Tony's Wiki

May 19 Notes

6 min read

References

Blue Book (Chapter 8) Temporal Logics in Computer Science:

The µ-calculus and Model Checking. Bradfield & Walukiewicz. Springer International Publishing, Cham (2018)

Recent survey

Green Book (Part V) Automata, Logics, and Infinite Games.

Selected proof, + history, good reference

Yellow Book (Chapter 6) Rudiments of µ-calculus. Arnold & Niwinski. Vol. 146. Elsevier (2001)

Abstract level

Proof Theory

Games for the µ-calculus. Niwinski & Walukiewicz. TCS 163(1&2):99-116 (1996)

On the Proof Theory of the Modal mu-Calculus. Studer. Studia Logica 89, 343-363 (2008)

Finitary Proof Systems for Kozen’s µ. Afshari and Leigh Oberwolfach Preprints. DOI 10.14760/OWP-2016-26 (2016)

Demystifying µ. Afshari et al. CoRR abs/2401.01096 (2024)

To find reference for other ppl’s work

Motivating example:

reactive systems Want to verify – Liveness Good things eventually happen – Safety Bad things never happen

permanent properties — requires fixpoint

Syntax and Seantics

We are talking about multiple-world property (model may change / future … ) One can extend propositional logic by adding two unary predicates:

  • [] : box; necessarily
  • <>diamond; possibly

Semantics: a transition systems with

  • states (a.k.a world)

  • relation

  • function interpreting atomic propositions

  • T, s |= [] Psi iff for every s -> t we have T, t |= Psi

  • T, s |= <> Psi iff for some s -> t we have `T, t |= Psi“

Satisfiability via tableaux

  1. construct negation normal form (not a restriction on expressive power) (negation on atomic P’s)

Every formula of modal logic is equivalent to one in NNF. The equivalence is provable in K.

  1. Looking at the rules, look for consistent successors for each note,
  2. A tableau: a tree where each node is labelled by a subset of Sub(Psi)

A tree is a special case of a Kripke structure

A path through tree t is a function P : N →S such that (currently P is not total, since path is in the tree)

A pre-tableau

The mod-rule can be applied only if no other rule is applicable

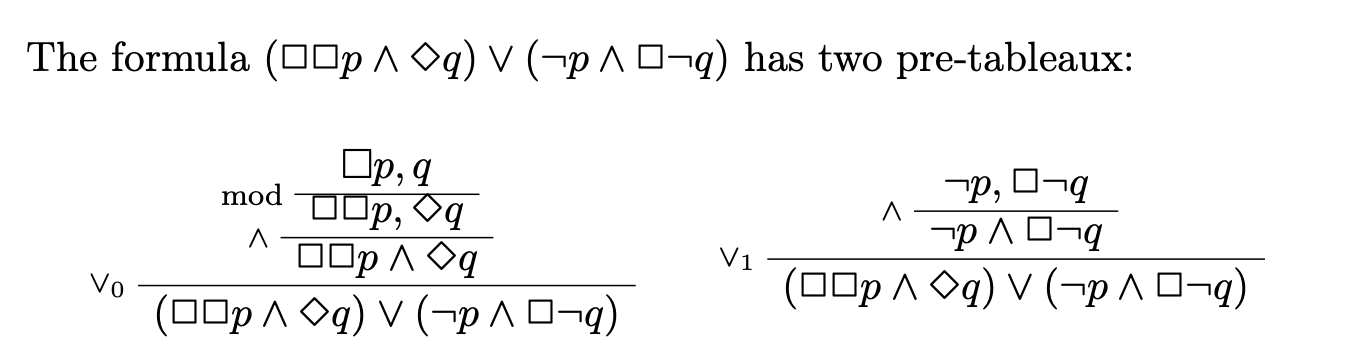The model of 1: w0 ---> w1 (q) The model of 2: w0 (neg p)

Each model rule go through, results in an extra node

Every formula of modal logic has at least one (and finitely many) pre-tableaux.

A tableau is a pre-tableau where the sequent (finite set of formulas) at each leaf has the form []Γ,Θ where Θ ⊆Lit is consistent.

Lemma (Soundness) If φ has a tableau then φ is satisfiable.

Visualization of the lemma: collapse the path separted by application of the mod-rules into the conditions into a Kripke structure.

Lemma (Completeness) If φ is satisfiable then φ has a tableau. Proof idea: satisfiable => T, s0 |= Psi,

  • Use the model T as a guiding tool to construct a tableau for φ.
  • We can argue that we can create a tableau

Corollary

  • Modal logic has the finite model property.
  • Decidable

exercise

Linear Time Temporal Logic

Modal language: a formula fixed the length of path of a model. e.g. <>^100 P

We need path quantification

  • X \phi, next, same as modal logic

  • \phi U \psi: \phi holds until \psi becomes true

  • F \phi: eventually true

    • true at some point in the future
    • F \phi = true U \phi

  • G \phi: always true

    • (at every point in the future, including present)
    • G \phi = !F !\phi

Other examples:

  • Recurrence: “p1 holds infinitely often”

    • G (F p1)

  • Request-response: “It is always the case that whenever p1 holds, p2 will hold sometime later”

    • G (p1 -> X F p2)

  • Fairness: “If p1 is true infinitely often, then so is p2

    • `G F p1 →G F p2

Semantics

check see slide

Linear vs Branching

LTL Proof Systems:

  •  in two-sided sequent calculus so we can handle negation.

  • φ U ψ ≡ ψ ∨ ( φ ∧ X (φ U ψ)) - unraveling once,

  • == ψ ∨ φ and ψ ∨ X (φ U ψ)

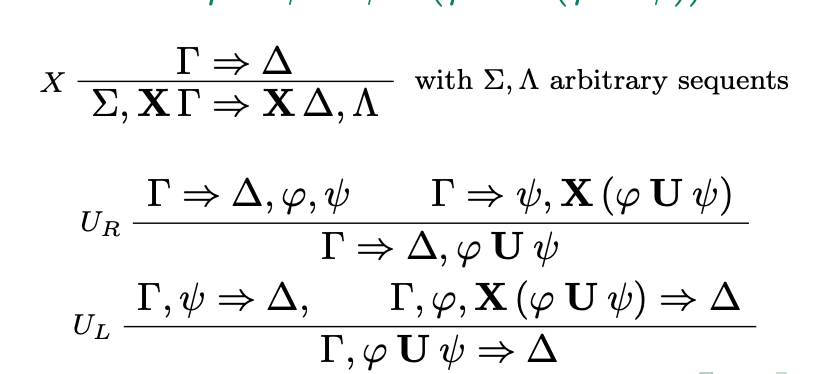
    • X: modality rule for next operator (recall modal logic)
    • UR and UL are just exploiting the unraveling equivalence
      • UR, applying the distr+unraveling
      • UL, applying the unraveling

Two sided sequent calculus (for satisfiability) gamma_1, ... , gamma_n |- delta_1, ... , delta_m means /\ gamma_i implies \/ delta_j

One sided: When reading as satisfiablity, we interpret comma as conjunction When reading as validity, we interpret comma as disjunction

The complexity of UR premise becomes larger =⇒ Infinite branches

Non-wellfounded Proofs

Proofhood condition every infinite path carries an infinite trace that passes through UL with the until formula principal.

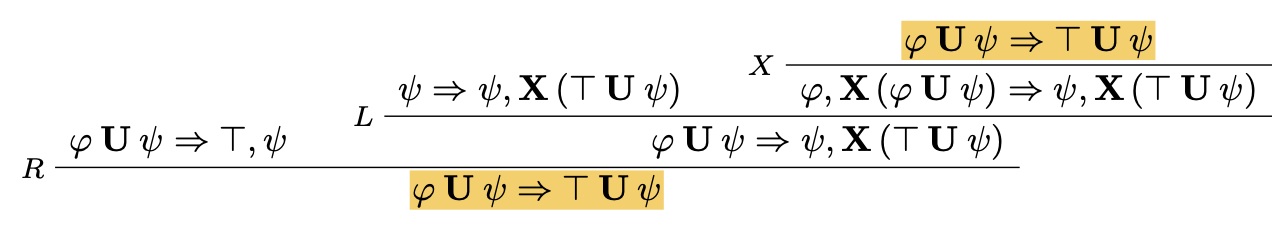
Hilbert’s LTL finitary axiomatisation (for comparison)

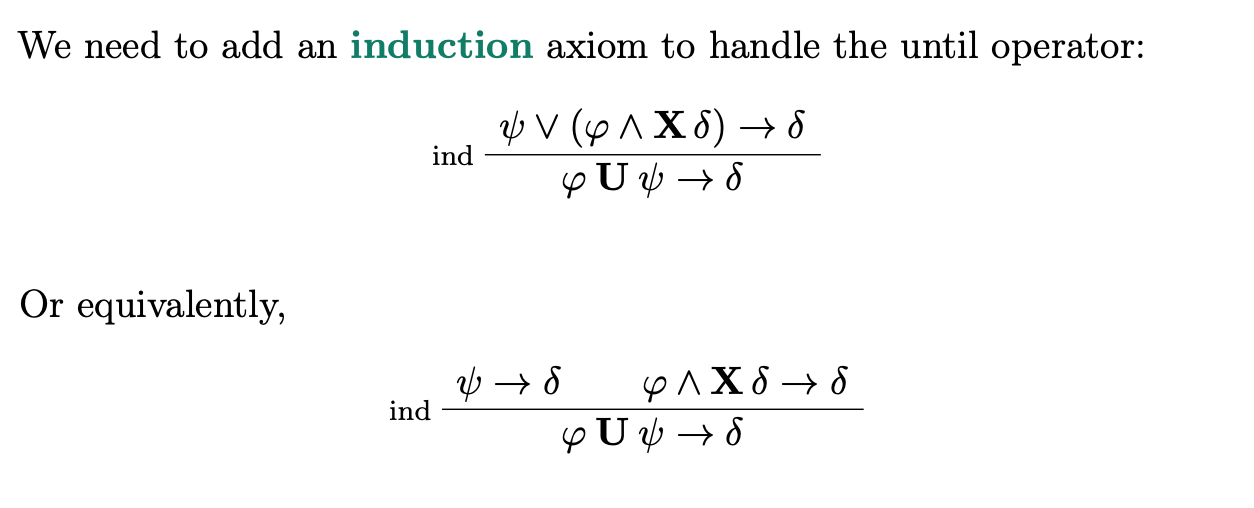
Cyclic and Ill-founded Proofs

For modal logic K4, we cannot derive Löb’s axiom: []([]p -> p) -> []p.

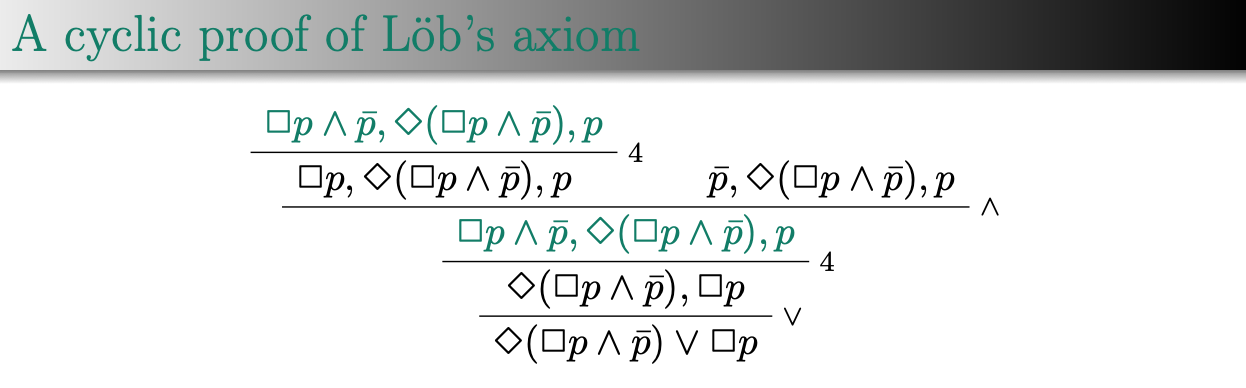something we cannot do wihout Lob axiom

Definition for cyclic:

  • on each cycle progress is made
    • For modal logic, <> rule is used
  • idea behind: the more general “principle of infinite decent”

Modal mu-calculus

Modal logic - revisited

  • syntax
  • semantics: denotations of formula: all the states that satisfy
  • Expressive limitation: properties along arbitrary (finite or infinite) paths in a structure cannot be presented
    • No infinite disjunctions like: <>1 p \/ <>2 p \/ .... (reachable)

Observation: they are just fixpoints of a function :x |-> p \/ <> x

  • syntax: add variable, mu and nu quantifiers We can express many modal operators using fixpoints
  • fixpoints back to back: infinitely often …
    • p is always reachable: mu y. (p \/ <> y) is independently evaluated, weakly binded, so p might not necessarily be on the particular path

Hierarchies in mu-calculus

fixpoints back to back #idea nested recursion

Connexion:

  • LTL can be captured by µ-calculus formulas of depth 2
    • why the extra depth? (exercise)
      • we have until, next
  • CTL, PDL can be captured by alternation-free µ-calculus
  • CTL*: depth 3

Connection (good properties)

  • Expressive: LTL, PDL, CTL, CTL*
  • Robustly decidability: model checking, satisfiability
  • Closed under bisimulation — but logic is not compact.
  • Equivalent to: alternating parity automata, parity games

automata (see Green block) simplify proofs and give more results

Tree Model Property: every satisfiable formula has a tree model.

Finite Model Property: every satisfiable formula has a finite model

Proof systems

Kozen’s axiomatization

neg(Psi) ----> Phi(neg(Psi))
-----------------
neg(Psi) ----> Nu x. Phi

leads to the (ind) axiom

we want to throw away the (ind) rule

using the ideas of tableaux …

The introduced rule (mu) and (nu) can form a derivation with direct correspondence to the traces

Result: For every infinite trace there exists a formula σxφ that appears infinitely often and is the shortest formula occurring infinitely often. ⇒ We call “most significant formula”

Graph View

Backlinks