Tony's Wiki

Automata on infinite structures

3 min read

Alternating automata

Nondeterminism = disjunctions

  • universal choices = conjunctions
q -->a {q1, q2} , q -->a { q3 }

or symmetrically, to a boolean frmula
q -->a (q1 /\ q2) \/ q3

or, disjunctive states, conjunctive states, eps-transutuibs

but we take the boolean formula form

With priorities

q --->a:1 (q1 /\ q2) \/ q3

Semantics

Run-view

  • a run is an infinite tree
  • Accepts if every branch is Parity accepting

again, we lost the nice symmetric of conj / disj

Game-vision

  • A(w) is a parity game
    • Positions
    • = prefix of words + boolean formula of the states
    • Moves: (aw, q) ---->p (w, b) where q ---->a:p b
    • falsifier: (w,b0 ∨b1) →(w,bi),i∈{0,1}
    • verfier:(w,b0 ∧b1) →(w,bi),i∈{0,1}
    • results in an infinite path
    • verifier wins if the path is Parity accepting
  • w is in L(A) if verifier wins A(w)
  • Verifier strategy= run tree (previous view)

Exercise:

Alternating coBüchi automaton for {wait, req, grant}: Every grant is eventually followed by a request.

Every suggests universal quantification, we should exploit it

If we take the view of falsifier (something not in the language)

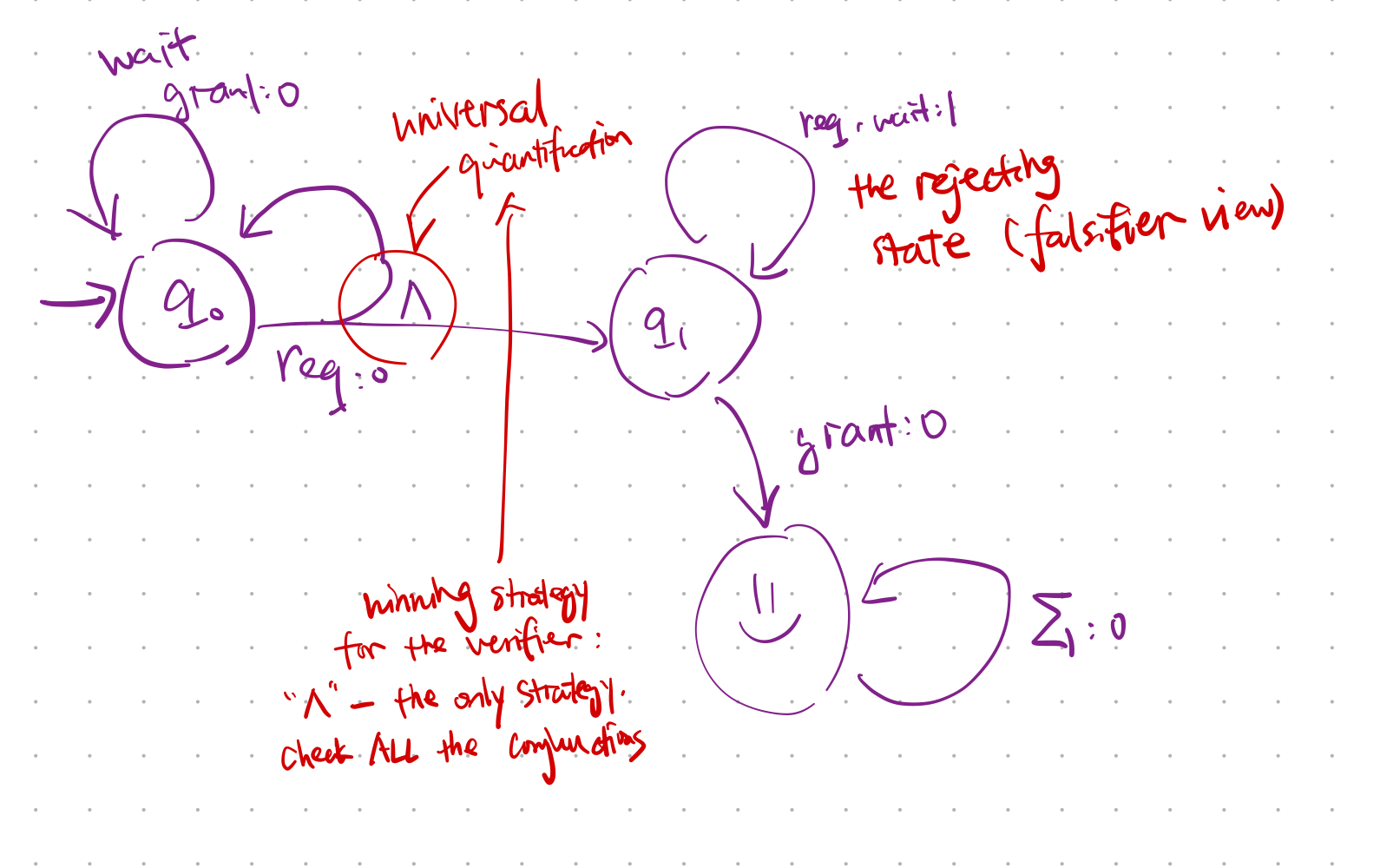
  • verifier: take /\ as conjunction, \/ as strategy to choose, to get a winning strategy
  • falsifier: take \/ as strategy to choose (disjunction), /\ as conjunction, to get a winning strategy
    • e.g. For req-grant-req-wait^omega, it has to wait a round at q0 so it falls into the rejecting loop at q1, otherwise, it goes to :) state and it loses

Trade-offs

following are equally expressive

  • alternating weak automate (SCC are accepting or rejecting)
  • Nondeterministic Buchi automata
  • determisistic parity automata

Encoding mu-calculus

revisit

Finite state automata over infinite trees

Infinite trees

  • Labelled unordered trees
    • NO root to be distinguished
  • Unfolded rooted graphs
  • (V, E, l : V → Σ)
    • V: nodes
    • E: edges
    • l: color functions

Relation to mu-calculus

  • [ ] p = accept from p in all successors (in the tree)
  • <> q = accept from p in some successor (in the tree)
  • Transitions: DNF formula over { <>q, []q | q \in Q }
    • `q ⇒ a (<> q1 /\ <> q2) / [] q3“

Semantics via parity games?

check

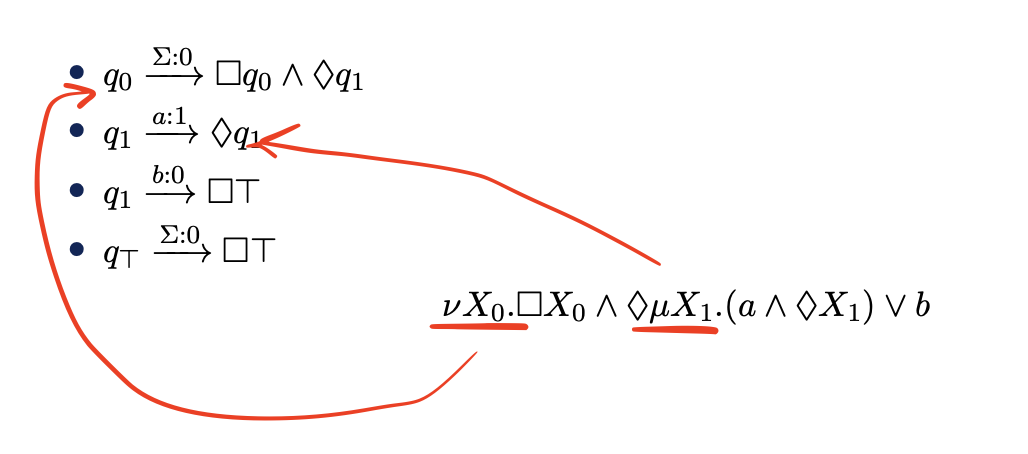Meaning: From everywhere b is reachable Falsifier: [ ] q0 find where b is non-reachable Verifier: <> q1 to navigate to the reachable state

Formula ComponentsAutomaton Concepts
FormulaAutomaton
SubformulasStates
♦, □ (Diamond, Box)Transitions
μ, ν (Fixpoint Operators)Priorities
Nested Fixpoint SemanticsParity Condition

Intuitive equivalence (as seen above), but…

  • Annoying details
    • •Automata are often defined on ordered binary trees (v.s. arbitrary/infinite branching)
    • •Nondeterminism is neater on ordered binary trees
    • •Labels on nodes vs. edges, <a>,[a] vs. ♦,□
    • •Size of a formula/automaton?

A classic for a reason

  • Highly expressive
    • subsumes CTL, bisimulation invariant MSO…
    • cf May 19 Notes
  • Highly decidable

Remark:

A strong foundation for extended models

Especially in the case of words:

  • Infinite alphabets
  • Infinite memory (counters, stacks…)
  • Quantitative models And for cyclic proofs?

Graph View