Higher-order languages and parity automata

Author: Paul-André Melliès Event: Ecole de Printemps en Informatique Théorique (EPIT) Theme: (Co)inductive & circular reasoning in programming, proofs and verification Date: May 19-23, 2025 Source: Aussois Slides

---

Introduction: Game Semantics

• Core Idea: Every proof of a formula A initiates a dialogue where Proponent tries to convince Opponent, and Opponent tries to refute Proponent. This provides an interactive approach to logic and programming languages.
• Linear Logic: Viewed through the lens of game semantics.

Example: The Drinker Formula

• Formula: $\exists y.\{A(y)\Rightarrow \forall x.A(x)\}$
  • Meaning: In a non-empty café, there exists a customer y such that if y is drinking, then all customers x are drinking.
• Provable in classical logic, but not in constructive logic.
• Proof Interpretation (Winning Strategy):
  1. Prover picks a random customer y.
  2. Refutator contradicts by finding a customer x who is not drinking while y is.
  3. Prover changes their witness to $y^{\prime }=x$ (the customer exhibited by Refutator).
  4. Refutator must admit defeat; Prover wins.

I have to win in one of the two games

Duality in Game Semantics

• Proponent (Program) plays the game A.
• Opponent (Environment) plays the game A (or A⊥).
• Negation permutes the roles of Proponent and Opponent.

---

Logical Connectives in Game Semantics

We can build new games

• Sum (Constructive Disjunction):
  • Proponent selects the board to be played.
  • Symbol: $\oplus$

The winning strategy becomes a choice what game to be played (or)

• Product (Constructive Conjunction): Opponent selects the board to be played.
  • Symbol: &

By de morgan, we can flip the roles of Proponent and Opponent Winning strategy: I need to know the best strategy for TWO games — (and)

• Tensor Product (Classical Conjunction): Two games played in parallel. Opponent can switch boards, but Player cannot.
  • Symbol: $\otimes$

In order to win the game, you have to be really strong, to play both games well — classical conjunction

• Parallel Product (Classical Disjunction): Two games played in parallel. Player can switch boards, but Opponent cannot.
  • Winning means win on either of the two boards.
  • Symbol: $\text{parr}$ (often represented by \invamp or \parr in LaTeX, or as an upside-down &)

We have the scheduler, ask Polgar to play a move, I can go to Carlsen play the same move, after Carlsen played, I can go back to Polgar and play the same move. … Can win by playing Polgar against Carlsen — copycat strategy

• Law of Excluded Middle: $A\text{parr}\neg A$. Player wins by playing one game (e.g., Polgar) against the other (e.g., Carlsen).

Note: the four connectives have a relation to linear algebra

Exponential Modality (!)

• Opponent opens as many copies as necessary to beat Proponent but is not allowed to open an infinite number of copies.

Give great power to the opponent to choose his strategy (oppenent can really explore the game). At the end we can say the opponent have a really good approximation of how I play. The hardship for me: I have to win each game as the opponent opens new copies and get better The only good news: not allowed to open

• Coinductive from Player’s view, inductive from Opponent’s view.

opponent should decide at some point to stop

• Isomorphism: $!A\otimes !B\cong !(A\&B)$. This is reminiscent of $\rho A\times \rho B\cong \rho (A+B)$ and is the origin of the name “exponential modality”.

In classical logic, the player can backtrack using the exp. modality (see drinker)

---

Tensorial Logic and Linear Continuations

• A primitive logic of tensor, sum, and negation.

Continuations

nat * nat => nat

Currently, bot can be viewed as any type, later we will see they are related to automata

(nat ⇒⊥) ⇒⊥ × (nat ⇒⊥) ⇒⊥ × (nat ⇒⊥) ⇒ ⊥

by viewing as sequential algorithms:

• Captures the difference between function-style operations and sequential algorithms.
  • Example: Left-to-right vs. Right-to-left addition.
    • lradd = $\lambda \phi .\lambda \psi .\lambda k.\phi (\lambda x.\psi (\lambda y.k(x+y)))$
    • rladd = $\lambda \phi .\lambda \psi .\lambda k.\psi (\lambda y.\phi (\lambda x.k(x+y)))$

The double negation of encoding nat can be viewed as question (program) and answer(player, environment)

time frame:
¬¬nat × ¬¬ nat ⇒ ¬¬nat
                question
question
12       
        question
            5
                    17

Tensorial Logic:

* A logic of tensor, sum, and negation.
* Linear logic without $A \cong \neg\neg A$.
* The syntax of linear continuations and dialogue games.

• Formulas: $A,B::=0|1|A\oplus B|A\otimes B|\neg A$.
• Sequents: $A_1,...,A_k⊢B$.
• Key Rules:
  • Axiom: $A⊢A$
  • Cut: $\frac{\Gamma ⊢AA,\Delta ⊢B}{\Gamma ,\Delta ⊢B}$
  • Negation Left
  • Negation Right: $\frac{\Gamma ,A⊢\perp }{\Gamma ⊢\neg A}$
  • Exchange
  • Tensor Left: $\frac{\Gamma ,A,B⊢C}{\Gamma ,A\otimes B⊢C}$
  • Tensor Right: $\frac{\Gamma ⊢A\Delta ⊢B}{\Gamma ,\Delta ⊢A\otimes B}$
  • Sum Left: $\frac{\Gamma ,A⊢C\Gamma ,B⊢C}{\Gamma ,A\oplus B⊢C}$
  • Sum Right (L/R): $\frac{\Gamma ⊢A}{\Gamma ⊢A\oplus B}$, $\frac{\Gamma ⊢B}{\Gamma ⊢A\oplus B}$
  • Units: $0⊢A$, $⊢1$, $\frac{\Gamma ⊢A}{\Gamma ,1⊢A}$

Now we have two way of prove (lradd way and rladd way): $\neg \neg A\otimes \neg \neg B⊢\neg \neg (A\otimes B)$

---

Functorial Approach to Proof Invariants

One application of category theory

Cartesian Closed Categories (CCCs)

• Brouwer-Heyting-Kolmogorov Interpretation:
  • Proof of $A\wedge B$ is a pair $(\phi ,\psi )$ of proofs for A and B.
  • Proof of $A\Rightarrow B$ is an algorithm $\psi$ transforming proofs $\phi$ of A into proofs $\psi (\phi )$ of B.

  What does algorithm mean? We should look at CCCs:

• A cartesian category $\mathcal{C}$ is closed if there’s a functor $\Rightarrow :{\mathcal{C}}^{op}\times \mathcal{C}⟶\mathcal{C}$ and a natural bijection ${\Phi }_{A,B,C}:\mathcal{C}(A\times B,C)\cong \mathcal{C}(B,A\Rightarrow C)$.

We can construct Free CCC from a category

• Free CCC:
  • Objects are formulas: $A,B::=X|A\times B|A\Rightarrow B|1$.
  • Morphisms are simply-typed $\lambda$-terms modulo $\beta \eta$-conversion.
  • $\beta \eta$-normal forms provide a “basis”.
• Simply-Typed $\lambda$-calculus Rules: Variable, Abstraction, Application, Weakening, Contraction, Exchange. With products: Pairing, Projections, Unit.
• Execution: $\beta$-rule: $(\lambda x.P)Q{⟶}_{\beta }P[x:=Q]$. $\eta$-rule: $P{⟶}_{\eta }\lambda x.(Px)$.
• Proof Invariants: Every CCC $\mathcal{D}$ induces a proof invariant $[-]$ modulo execution from free-ccc(C) to $\mathcal{D}$.

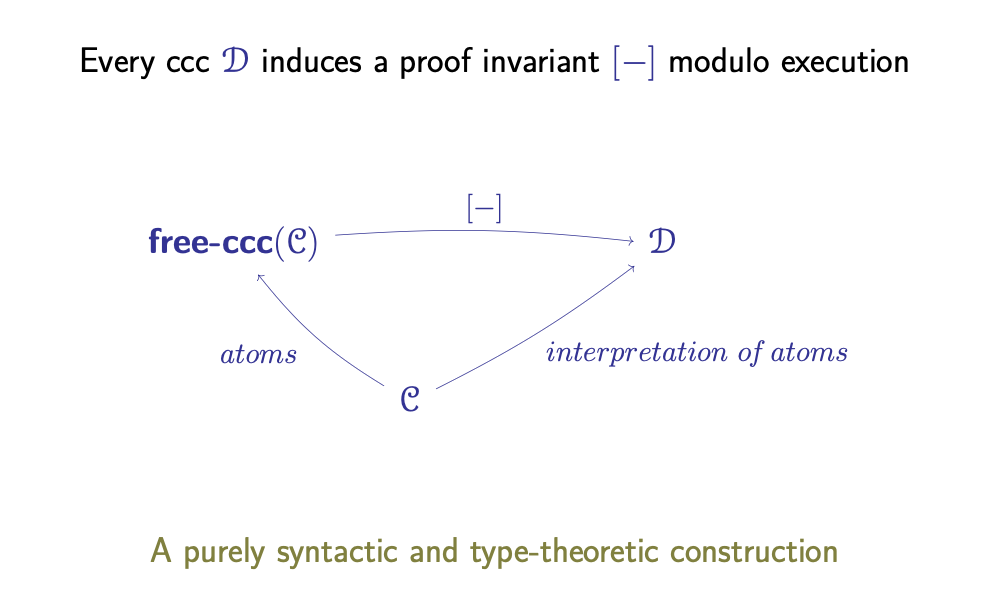
• $\mathcal{D}$ morphisms are just proof invariants in lambda terms (w.r.t. beta/eta ~ execution)

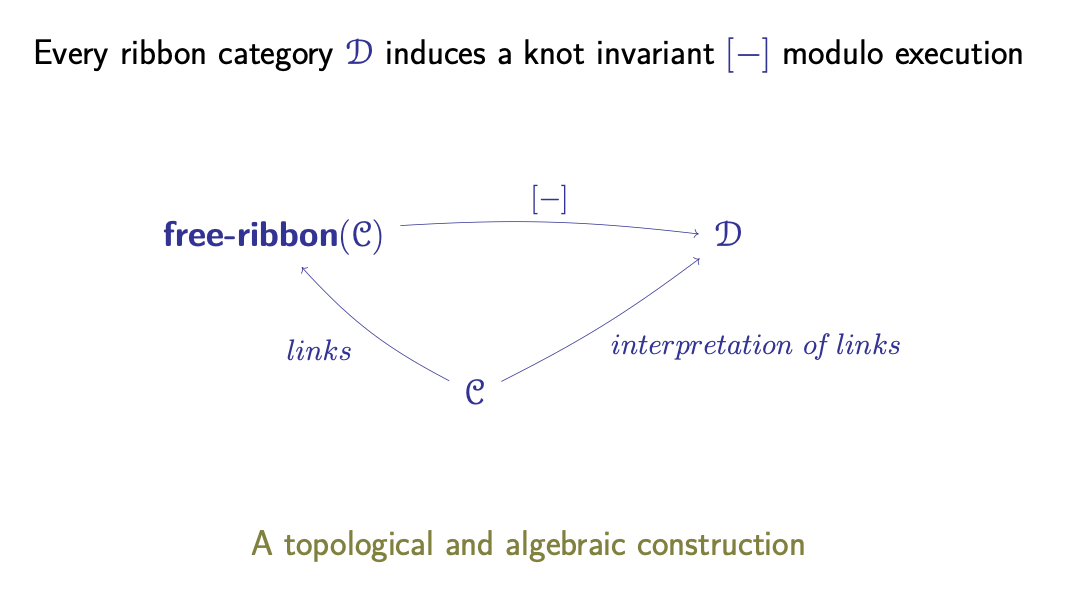
Analogy with Knot Invariants

• Every ribbon category $\mathcal{D}$ induces a knot invariant $[-]$ modulo deformation from free-ribbon(C) to $\mathcal{D}$.
• The free ribbon category is the category of framed tangles.

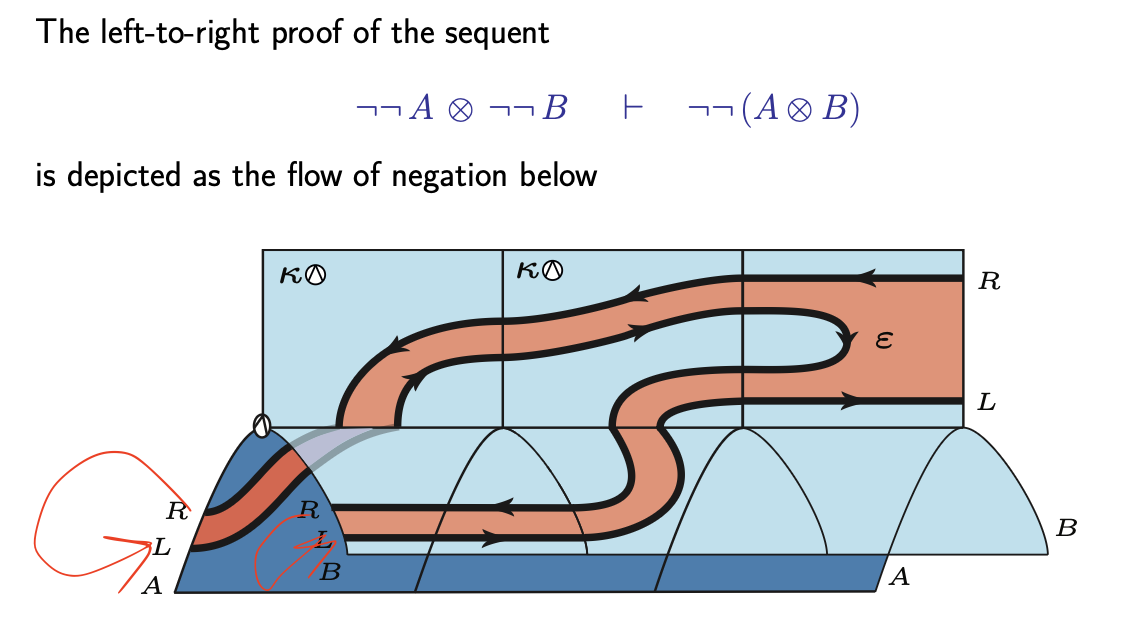
Proofs as 3D String Diagrams

• Example: Left-to-right proof of $\neg \neg A\otimes \neg \neg B⊢\neg \neg (A\otimes B)$ depicted as a flow of negation.

---

Dialogue Categories

Every CCC is a dialogue category

• The categorical counterpart of tensorial logic.
• Definition: A symmetric monoidal category $\mathcal{D}$ with:
  • An object $\perp$ (representing falsity or end of game).
  • A functor $A\mapsto \neg A:{\mathcal{D}}^{op}⟶\mathcal{D}$.
  • A natural family of bijections ${\phi }_{A,B}:\mathcal{D}(A\otimes B,\perp )⟶\mathcal{D}(A,\neg B)$.
• Dialogue Category with Finite Sums:
  • Underlying category $\mathcal{D}$ has finite sums.
  • Finite sums distribute over the tensor product.
    • $(A\otimes B)\oplus (A\otimes C)⟶A\otimes (B\oplus C)$ is an isomorphism.
    • $0⟶A\otimes 0$ is an isomorphism.

Free Dialogue Category $\mathcal{F}$ with Sums

• Objects: Formulas of tensorial logic ($0,1,A\oplus B,A\otimes B,\neg A$) modulo equations (associativity, unit laws, distributivity).
• Morphisms: Derivation trees of tensorial logic modulo equations.
• Every dialogue category with sums $\mathcal{D}$ induces a functor $[-]:\mathcal{F}⟶\mathcal{D}$ preserving logical structure (negation, sums, tensor products, units).

---

Dialogue Games

We keep the same formula, but view them as dialogue games no longer derivation trees, but “proof nets”

• The concrete data structure behind the logic.
• Key Theorem:
  • Objects of $\mathcal{F}$ are dialogue games generated by $A,B::=0|1|A\oplus B|A\otimes B|\neg A$.
  • Morphisms of $\mathcal{F}$ are total and innocent strategies.
  • Slogan: Innocent strategies are the “proof-nets” of tensorial logic.
• Correspondence (Normal Form): Every formula $A$ of tensorial logic is uniquely determined by a normal form $A={⨁}_{i\in I}{⨂}_{j\in J_i}\neg A_{ij}$.
  • Interpretation: $⨁$ (choice), $⨂$ (parallelism), $\neg$ (change of player).
• Rooted Dialogue Game: A bipartite tree $(C,V,▹)$ with nodes $C$ (cells) and $V$ (values).
  • $▹\subseteq C\times V+V\times C$.

value and cells will alernate in the tree path * Polarity function $\lambda :C+V⟶\{+1,-1\}$ such that: * $\alpha ▹v\Rightarrow \lambda (\alpha )=\lambda (v)$ * $v▹\alpha \Rightarrow \lambda (\alpha )=-\lambda (v)$ * Root $\ast$ of the tree is a value of polarity +1.

• Dialogue Game: A family of rooted dialogue games $A=(A_i|i\in I)$.
• Operations on Dialogue Games:
  • Sum ($A\oplus B$): Putting families of rooted games side-by-side. Every dialogue game is the sum of its rooted components $A={⨁}_{i\in I}{A}_i$.
  • Negation ($\neg A$): Transforms a dialogue game (family of roots) into a new rooted dialogue game by adding a new root connected to the original roots via “op” cells.
  • Tensor Product (${⨂}_{i\in I}\neg A_i$): Defined by coalesced sum of negated games (sharing a common root).
  • Every rooted dialogue game is a tensor product of negated games $A={⨂}_{i\in I}\neg B_i$.
  • Hence, every dialogue game is of the form $A={⨁}_{i\in I}{⨂}_{j\in J_i}\neg A_{ij}$.
  • Tensor distributes over sum: $A\otimes ({⨁}_{i\in I}{B}_i)={⨁}_{i\in I}(A\otimes B_i)$.

Positions of a Dialogue Game

• The underlying asynchronous transition system.
• $Pos(0)=\varnothing$
• $Pos(1)=\{\ast \}$
• $Pos(A\oplus B)=Pos(A)+Pos(B)$
• $Pos(A\otimes B)=Pos(A)\times Pos(B)$
• $Pos(\neg A)=Pos(A)+\{\ast \}$
• Positionality Theorem (2004): Innocent strategies are positional.
• The set $Pos(A)$ defines a coherence space and an ordered set of positions.

Gödel Translation L $⊸$ LL+

• Suspension Modality ($\downarrow$): A symmetric monoidal comonad on a symmetric monoidal category $\mathcal{C}$.
• Every suspension modality $\downarrow$ induces an adjunction between $\mathcal{C}$ and its category $\mathcal{D}$ of $\downarrow$-coalgebras.
• When $\mathcal{C}$ is $\ast$-autonomous, $\mathcal{D}$ is a dialogue category with negation $\neg A=Free((\text{Forget }A{)}^{\ast })$.
• This induces a functor from $\mathcal{F}$ to $\mathcal{C}$ mapping logical connectives appropriately (e.g., $[\neg A]=\downarrow ([A{]}^{\ast })$).
• Functorial Interpretations: $\mathcal{F}\to Rel$, $\mathcal{F}\to Coh$, $\mathcal{F}\to ScottL$.

---

Types as Sets of Positions

• Positions can be seen as states in a higher-order automaton or intersection types specifying $\lambda$-term behavior.

Church Encoding of Data Types

• A functional encoding of words and trees.
• Natural Numbers:
  • Based on the induction principle: $\forall n.(\psi (n)\Rightarrow \psi (n+1))\Rightarrow (\psi (0)\Rightarrow \forall n.\psi (n))$.
  • Removing first-order part: $(\psi \Rightarrow \psi )\Rightarrow (\psi \Rightarrow \psi )$.
  • Church encoding type: $(o\Rightarrow o)\Rightarrow (o\Rightarrow o)$.
  • Zero: $\lambda S.\lambda z.z$
  • One: $\lambda S.\lambda z.Sz$
  • There’s a one-to-one correspondence between $\lambda$-terms of type $(o\Rightarrow o)\Rightarrow (o\Rightarrow o)$ (up to $\beta \eta$) and natural numbers.
• Finite Words:
  • Type: $(o\Rightarrow o)\Rightarrow (o\Rightarrow o)\Rightarrow (o\Rightarrow o)$ (for an alphabet of two letters).
  • Example aba: $\lambda a.\lambda b.\lambda c.a(b(a(c)))$.
  • One-to-one correspondence with finite words $w\in {\Sigma }^{\ast }$.
• Finite Trees:
  • Type (e.g., for signature $\{a:2,b:1,c:0\}$): $(o\times o\Rightarrow o)\Rightarrow (o\Rightarrow o)\Rightarrow (o\Rightarrow o)$.
  • Example: $\lambda a.\lambda b.\lambda c.a(c,a(b(c),c))$.
  • One-to-one correspondence with finite trees on the signature.

Church Encoding in Linear Logic

• Arrow type $A\Rightarrow B$ factors as $!A⊸B$.
• $A⊸B=A^{\perp }\text{parr}B=(A\otimes B^{\perp }{)}^{\perp }$.
• A tree can be typed with $!$ on arguments (e.g., $!o⊸(!o⊸o)$) or more linearly (e.g., $o⊸(o⊸o)$).
• Duality:
  • Proponent (Program) plays $A$; Opponent (Environment) plays $A^{\perp }$.
  • Dual of a tree is a tree automaton.
  • Counter-formula for trees $B^{\perp }=!(o⊸o⊸o)\otimes !(o⊸o)\otimes o\otimes o^{\perp }$ is the type of tree automata.
  • Counter-formula $A^{\perp }$ (with more !) is type of alternating tree automata.

---

Higher-Order Automata

• Goal: Define recognizable languages for sets of simply-typed $\lambda$-terms.
• Approach: Use a finite Scott domain interpretation of types (after Salvati).

Scott Semantics of Linear Logic

• A preorder $(Q,\le )$ induces a Scott domain $(Dom(Q),\subseteq )$ where elements are lower sets of $Q$.
• If base type o is interpreted as $Dom(Q,\le )$, then any type $A$ is interpreted as $Dom(Q_A,{\le }_A)$ for some preorder $Q_A$ of higher-order states.
• Logical Connectives on Preorders:
  • $A^{\perp }:=A^{op}$
  • $A\&B:=(A+B,{\le }_A+{\le }_B)$
  • $A\otimes B:=(A\times B,{\le }_A\times {\le }_B)$
  • $!A:={\mathcal{P}}_{fin}(A)$, with order $\{a_i\}{\le }_{!A}\{b_j\}⟺\forall i\exists j.a_i{\le }_A{b}_j$.
• Preorder of Higher-Order States ($Q_A$):
  • $Q_{A\times B}=Q_A\&Q_B$
  • $Q_{A\Rightarrow B}=!Q_A⊸Q_B$ (linear implication maps to tensor product like structure for states). A state for $A\Rightarrow B$ is like $\{q_1,...,q_n\}⊢q$.

Definition: Higher-Order Automaton

A higher-order automaton $\mathcal{A}=⟨\Sigma ,A,Q,\delta ,q_0⟩$ consists of:

• A higher-order alphabet $\Sigma =\{a_1:A_1,...,a_n:A_n\}$ where $A_i$ are simple types (arities).
• A simple type $A$ (the language’s type).
• A finite preordered set of states $Q$.
• Transition functions $\delta (a_i)\subseteq Q_{A_i}$ (using the $Q$ for atomic states in $A_i$).
• An initial higher-order state $q_0\in Q_A$.

Run-Trees

• A run-tree $R$ is a derivation tree of the judgement $⟨\Sigma ⊢M:A|\delta ,q⟩$ in an intersection type system.
• Key Rules for Run-Trees (Intersection Types):
  • Variable: $\frac{q{\le }_A{q}^{\prime }{q}^{\prime }\in \delta (a)}{⟨\Sigma ,a:A⊢a:A|\delta ,q⟩}$ (simplified)
  • Abstraction: $\frac{⟨\Sigma ,a:A⊢M:B|\delta \cup \{a\mapsto \{q_1,...,q_n\}\},q⟩}{⟨\Sigma ⊢\lambda a.M:A\Rightarrow B|\delta ,\{q_1,...,q_n\}⊢q⟩}$ (simplified, using $⊢$ for state form)
  • Application: $\frac{⟨\Sigma ⊢M:A\Rightarrow B|\delta ,u⊢q⟩⟨\Sigma ⊢N:A|\delta ,u{⟩}_i}{⟨\Sigma ⊢App(M,N):B|\delta ,q⟩}$ (where $u$ is a set of states for N)
  • Bag: $\frac{⟨\Sigma ⊢M:A|\delta ,q_1⟩...⟨\Sigma ⊢M:A|\delta ,q_n⟩}{⟨\Sigma ⊢M:A|\delta ,\{q_1,...,q_n\}⟩}$

Adequacy Theorem (for $\lambda$-calculus)

• Given a finite preorder $(Q,\le )$.
• The interpretation $[[M]]$ of a simply-typed $\lambda$-term $M$ of type $A$ coincides with the set of its accepting states.
• $q\in [[M]]⟺M\text{ is accepted by the automaton }⟨\varnothing ,Q,A,\varnothing ,q⟩$.
• Corollary: Acceptance property is decidable.

---

Higher-Order Recursion Schemes (HORS)

• From finite to infinitary lambda-calculus.
• Example: $S\to Fabc$, $Fxyz\to x(yz)(Fxy(yz))$ generates an infinite tree.
• Can be seen as a $\lambda$-term of a specific type in simply-typed $\lambda$-calculus with a recursion operator $Y$.
  • E.g., $S\to Fc$, $F\to \lambda x.ax(F(bx))$ can be $M=(Y[\lambda F.\lambda z.az(F(bz))])c$.
• This produces an infinitary $\lambda$-term $[M{]}_{\infty }$.
• Generation by infinitary $\beta$-rewriting: $[M{]}_{\infty }⇝N$ (infinite tree).
  • The sequence of $\beta$-reductions can be chosen “strongly Cauchy convergent”.

Invariance Theorem

• For a strongly Cauchy convergent infinite $\beta$-reduction sequence $M⇝N$:
  • The HO-automaton $\mathcal{A}$ recognizes $M⟺$ the HO-automaton $\mathcal{A}$ recognizes $N$.
• This is easy for automata with purely inductive acceptance but needs revisiting for mixed inductive/coinductive conditions.

---

Higher-Order Automata with Boundary

• Shifting to infinitary trees and $\lambda$-terms.

The $\lambda Y\mu \nu$-calculus

• Simply-typed $\lambda$-calculus with least ($Y_{\mu }$) and greatest ($Y_{\nu }$) fixpoint operators.
• Syntactically behave same: $Y_{\mu }M\to M(Y_{\mu }M)$, $Y_{\nu }M\to M(Y_{\nu }M)$.
• Interpreted differently in Scott semantics $[[-]{]}_{\mu \nu }$.

Infinite $\lambda$-terms with Boundary

• A boundary $\partial M$ of an infinitary $\lambda$-term $M$ is a set of infinite paths of $M$.
• An infinitary $\lambda$-term with boundary is $(M,\partial M)$. (Inspired by Borelian games).

Adequacy Theorem with Boundary

• The interpretation $[[M]{]}_{\mu \nu }$ of a $\lambda Y\mu \nu$-term $M$ coincides with its set of accepting states.
• $q\in [[M]]⟺M\text{ is accepted by automaton }\mathcal{A}=⟨\varnothing ,Q,A,\varnothing ,q⟩$, where acceptance on run-trees reflects inductive/coinductive status of fixpoints.
• $Y_{\mu }P$: infinite path not in boundary.
• $Y_{\nu }P$: infinite path in boundary.

Invariance Theorem (with Boundary)

• For $M⇝N$ (strongly Cauchy convergent):
  • HO-automaton $\mathcal{A}$ recognizes $M$ with boundary $\partial M⟺\mathcal{A}$ recognizes $N$ with boundary $\partial N$.
• Tool: Diffraction Patterns: An occurrence $D$ of a $\beta$-redex $R$ in $M$ is turned into a diffraction pattern $E=\{D_{A,i}\}\cup \{D_B\}$ in $N$ by the reduction.

---

Modal Translation of Higher-Order Parity Games

• The S4 construction at work.
• Colour Modality (${◊}_n$) on Preorders: For $n$ colours, ${◊}_{n}A:=A\underset{n\text{ times}}{\underbrace{\&\dots \&}}A$.
  • $Dom({◊}_{n}A):=Dom(A)\times \cdots \times Dom(A)$ (n times).
• ${◊}_n$ defines a comonad that commutes with finite products.
• The composite modality $!{◊}_n$ defines an exponential modality of linear logic, making $Kleisli(Scott,!{◊}_n)$ a CCC.
• Inductive-Coinductive Fixpoint: For $n$ (even) colours, $Y(M)=\nu x_n.\mu x_{n-1}.\dots .\mu x_1.M(x_1,\dots ,x_n)$ defines an interpretation in $\lambda Y\mu \nu$-calculus.
• Collecting colours is like collecting levels of copies.

Parametric Modality (for Intersection Types)

• A family of functors ${\square }_m:\mathcal{C}\to \mathcal{C}$ for $m\in \mathbb{N}$, each lax monoidal, defining a parametric comonad.
• Relates to copy management in linear logic (e.g., $!A\to !!A$, $!A\to A$).

---

Conclusion and Future Works

• Higher-order automata generalize and explain higher-order model checking.
• A modal $\lambda Y\mu \nu$-calculus with boundaries refines the usual $\lambda Y$-calculus.
• Decidability proof based on Scott semantics of linear logic and infinitary rewriting theory.
• New automata-theoretic foundations for the lambda-calculus.

Not Discussed

• Profinite lambda-calculus (with van Gool, Moreau, 2023).
• Equivalence of syntactic (Hillebrand & Kanellakis 1996) and semantic (Salvati 2009) definitions of higher-order regular languages (Moreau & Nguyên, 2024).
• Dialogue duploids and classical L-calculus (with Mangel, Munch-Maccagnoni, 2025).
• Ongoing work on context-free grammars and Chomsky-Schützenberger theorem (with Zeilberger, 2022, 2025).