Tony's Wiki

Expressiveness of cyclic proofs

3 min read

Types with fixed points

Simple types + fixed points

  • appear positively
  • inductive + coinductive data types (mu and nu)

Sequent calculus with fixed points sigma1, ..., sigma n => tau : interpreted as prod sigma_i => tau

introduction / construct / LHS
...

elimination / destructed / RHS
=> pho
\sigma => \tau
--------------
\sigma -> \pho => \tau

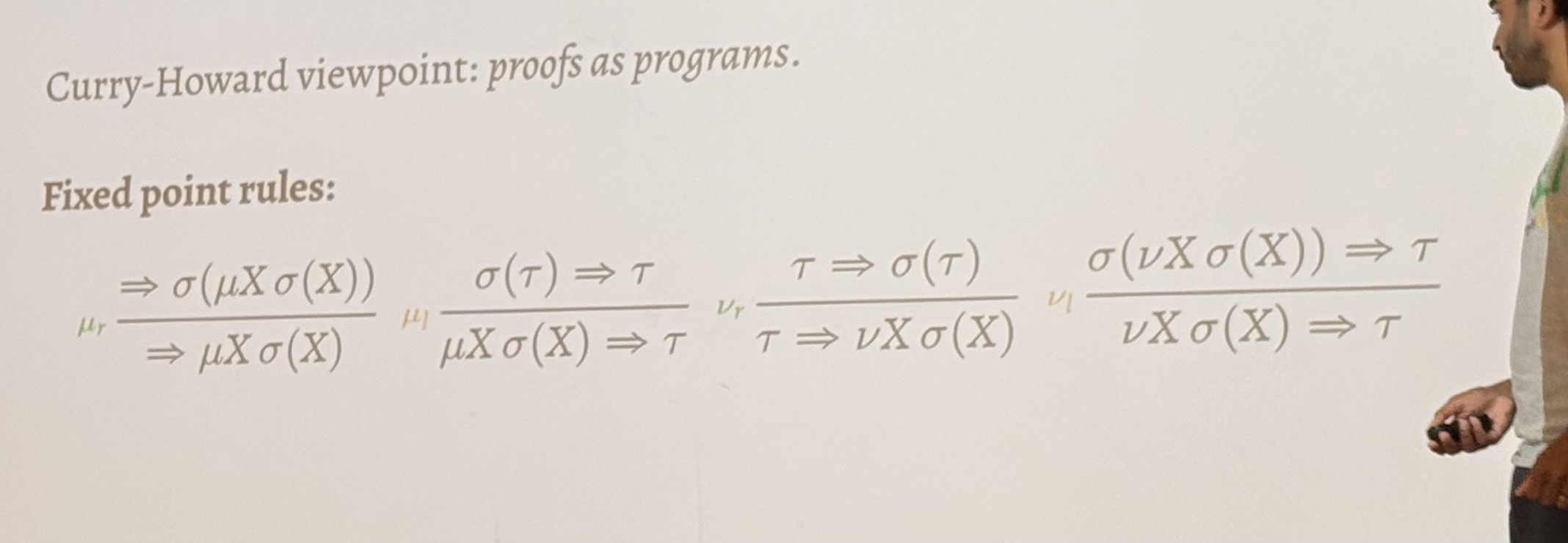
muLJ is the extension of usual LJ by the fixed point rules

  • computational theory given by cut-elimination

idea important the logical correspondence to the structural unfolding rules in mu-l

Example: natural numbers as inductive types

the destructor:

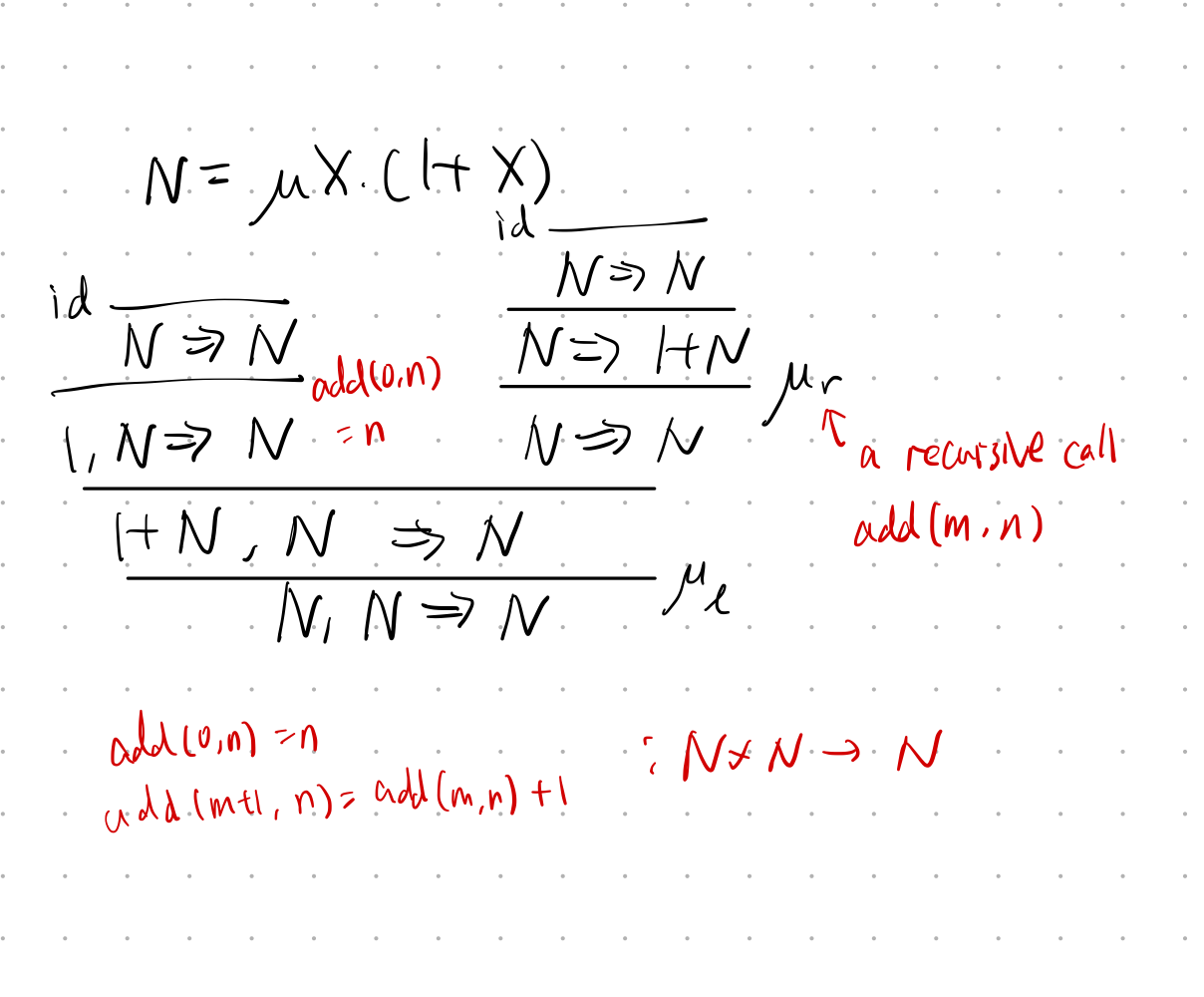
Example : streams as coinductive types

Aside: interpreting types wit fixed points

  • A set theoretic model?
    • cannot interpret fixed-point types
      • no nu X. X, mu X. ((X -> A) -> B)
      • non-canonicalizable meaning
  • A computability theoretic model:
    • interpret T as a set tau^R \in natural number (powerset of natural numbers, forming a lattice ⇒ LFP, GFP)
      • (Kleene model)
    • (sigma -> tau)^R = {n : \forall m in sigma^R, Mn(m) terminates \in tau^R}
      • a more abstract way
      • analogy to logical relations
    • (mu X. sigma(X))^R = LFP[A |-> \sigma(A)^R]

also extend to system F

Circular Proofs

Non-wellfounded typing:

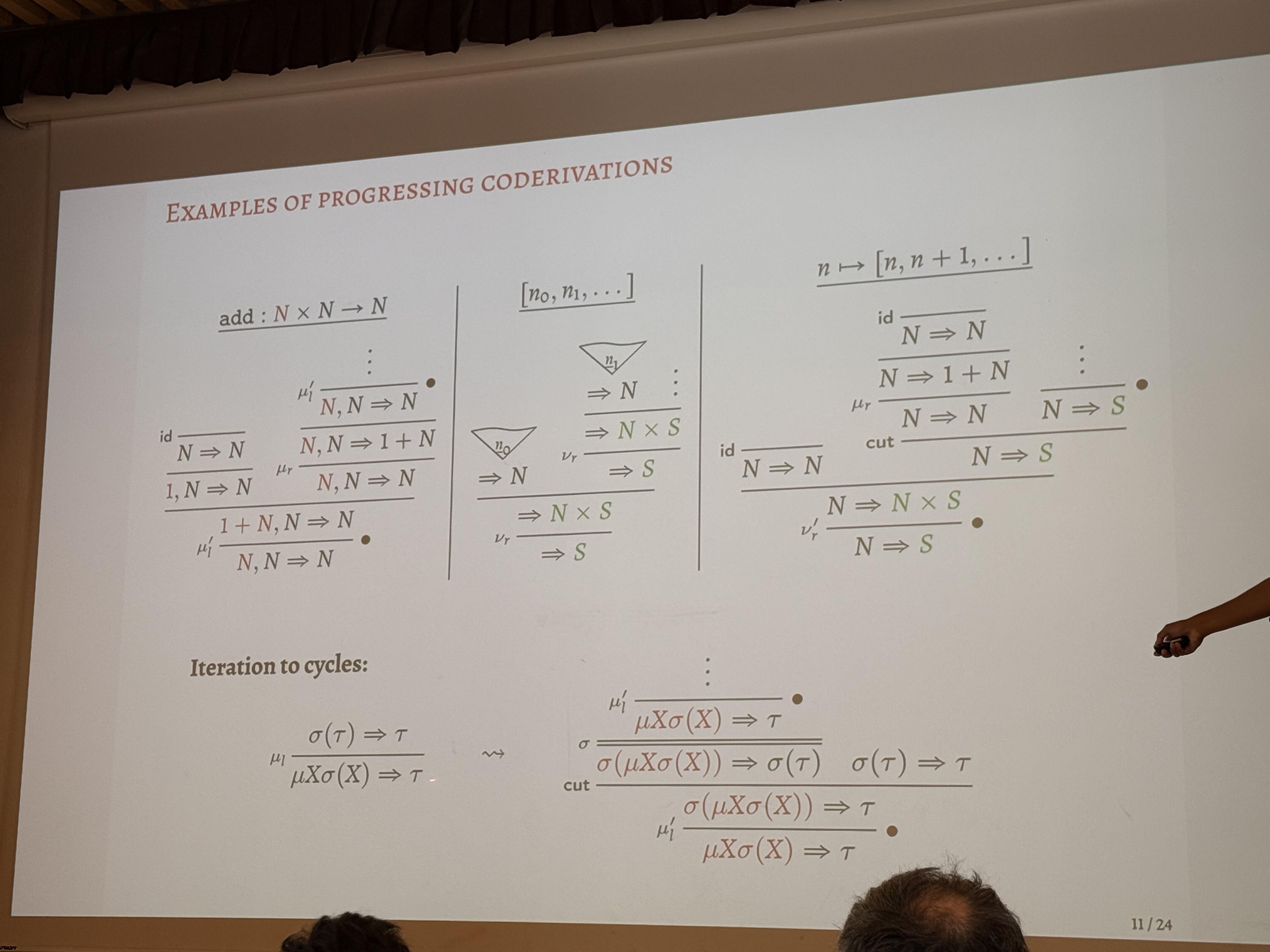
Progressing coderivations

NB: cyclic proof checking is decidable, reducing to universality of Buchi automata

  • no iterator anymore
  • we have unfolding, and the proof can be infinite

If you observe the proof tree, you will see a more fine grained correspondence to the algorithm. destructor on the left

The only infinite branching happens on mu-left and nu-right

We can encode mu-l! ( question ( strict?) more expressive)

Ackermann function

  • recall, non encodable in natural number primitive recursors - requires higher types
  • but we can use mu-l' to construct circular proof
    • unlike previous example, much complexer (with 3 infinite branch c.f. 1)
    • progressive is provable

Some observations

  • circular proofs interpret finite ones
  • circular proofs can be more succinct than finite ones but,

Are circular proofs more expressive than finite ones?

System T ( a focus of the above designs )

(C)T is the restriction of (C)muLJ to just one fixed point N

  • (C) for circular variant

Thm: (Affine) CT and (affine) T represent the same type 1 functions [KPP21]

How it fits with the Ackermann function?

Indeed, write (C)T_n for restriction of (C)T to just level n types.

Thm (Das21): T_n+1 and CT_n interpret each other, thus T_n+1 and CT_n represent the same type 1 functions

Totallity: the problem of non-constructivity

Proposition (Totality): If P is progressing then P^interp is total

  • the proof is highly non-constructive
    • proof by contradiction
    • we are building an infinite branch out of an infinite tree

What about (C)muLJ?

Theorem: CD23: muLJ and CmuLJ define just the functions provably recursive in Sigma

Motto: circular proofs are more expressive than finite ones … up to a point

Next part: model theory of circular proofs

Graph View