Basics of category theory (Farzard)

Introduction

monoid = element + binary operation (assoc + unit element)
- $e$ can be considered as a function from singleton to the set $η (⋆) = e$
- $μ : M \times M \to M$ , applying $\cdot$
We can do the same for groups: $δ : M \to M \times M$

Different structures can be presented by the same diagram in different categories.

Definitions

A metagraph:
- objects
- arrows
- dom: arrows → objects
- cod: arrows → objects
A metacategory is a metagraph s.t.:
- id
- $\circ$
- assoc of $\circ$
- unit law for $i d$ and $\circ$

Examples:

▶ Sets: Objects are all sets; arrows are all functions with the usual composition. ▶ Groups: Objects are all groups; arrows are all homomorphisms of groups. ▶ Topological spaces: Objects are all topological spaces; arrows are all continuous functions. ▶ Hausdorff spaces with continuous functions. ▶ All ringed spaces with their morphisms.

MetaCat → Cat

A directed graph (note that defined on set of objects, arrows, and composable pairs $\times_{O}$ of arrows)
A (small) category is a directed graph such that …
- Exercise: Is this definition just a monoid for the product ×O.

Is Sets a category?

Large Categories

We consider all the “small” sets Let $U$ be a big enough set, the universe, a set is small if $x \in U$

Set: all small sets, and all functions between them.
Pointed sets Set⋆: all small sets with one distinguished element ⋆, and all ⋆-preserving functions.
Mon: small monoids, and monoid morphisms. ▶ Grp: (small) groups, and group morphisms. ▶ Ab: (small) abelian groups, with morphisms of such. ▶ Rng: (small) rings, and ring morphisms. ▶ R-Mod: left modules over the ring R, and linear maps. ▶ Top: (small) topological spaces, and continuous maps.
Cat: small categories, and functors.
- A category is small, if set of its objects and the set of its arrows are both small.

Foundations

Set is not a small category
ZFC + existence of U suffices for the usual purposes of category theory
- One needs to define the notion of universe U in such a way that its properties ensure that any standard operation of set theory applied to elements of U will produce elements of U.
See here for more discussion

Functors

morphism of categories

preserves composition
preserves identity

Complete Category

Natural transformations

$θ : F - > G$ for functiors $F$ and $G$
- that satisfies the commutative diagram
An isomorphism is a natural transformation $θ$ such that $θ (X)$ is an isomorphism for all $X$ in the category.

How to build categories

Product of two objects

described by: forall $X$ in $C$ , there exists a unique arrow $p_{1} : X \to A$ and $p_{2} : X \to B$ such that $f = p_{1} \circ p_{2}$
can be extended to arbitrary number of objects

Terminal Object

of a category $C$ is just the empty product $⊤$

decsribed by: forall $X$ in $C$ , there exists a unique arrow $p : X \to ⊤$ such that $f = p \circ p_{1}$

Coproduct of two objects

e.g. Set = disjoint union of sets $A ⊔ B = (X \times 1) \cup (Y \times 2)$

Initial Object

the empty coproduct

Opposite category

idea: is the co/contravariant functor related to w\subtyping

Presheaf

A presheaf on a category C is a contravariant functor from C^op to Set. ⇒ Yoneda embedding

Products of categories

object = pair of (X, Y)
morphism = pairwise morphism

Example:

Covariant bifunctor from C^op X C -> Set sending (X, Y) to hom(X, Y)
The contravariant bifunctor from C^op X C -> Set sending (X, Y) to hom(X, Y)

can be encoded by compositions of unary functors on C^op and C

Right adjoint

A profunctor from D to C: C^op X D -> Set
- The hom bifunctor is a indentity profunctor C --/-> C … todo

Adjoint functors

a pair of adjoint functors between posets is a Galois correspondence
free: Set → Grp is the functor gives us the free group on a set
The forgetful functor Grp → Set is right adjoint to …

Functor Categories

objects are functors
morphisms are natural transformations

Comma Categories

objects are pairs of objects and morphisms
morphisms are morphisms that commute a diagram Set / * iso Set iso Set/ *

Remark 1: An object X : C can be view as a functor X : 1 -> C, so we can encode X / obj using X / functor

We can also define over a functor F : C --> D, X : D, define a new category X / F also dually for F / X

Also F/G category over category is definable

Remark 4 : a natural trasformation \theta : F -> G between 2 functors is just the same as a functor C → (F/G)

Syntactic Category & Category of models

Another way to build category: using logic and models

Theories      - (lambda terms, compilers between them )
  | A
  | |
  | |
  | |
  | |
  V |
Categories    - (category of category, ... )

Depending on the theory, we need to assume our category have extra properties: e.g. cartesian products, limits, has images, … (need to be looked from the theory)

Limits and Colimits

cone, cocone limit, colimit

Basics of Coalgebra

By Park and Milner, bisimulation as a notion of behavioural equivalence for concurrent processes
Aczel’s theory: lift the bisimulation to the level of arbitrary coalgebras

Algebras

= (carrier) sets with operations e.g.: Nat + zero, succ $[zero, s u cc] : 1 + N a t \to N a t$ : take a set add one extra element to it

e.g. ${0, 1}$ with operations zero and flip $[zero, f l i p] : 1 + {0, 1} \to {0, 1}$ : take a set add one extra element to it

Algebras for a functor

Definition. Let $F : C \to C$ be a functor, An F-algebra is a pair $(X, α)$ consisting of an object $X$ of $ma t h c a l C$ and a morphism $α : F (X) \to X$ in $C$ .

Example: M-algebra defined by $MX = 1 + X$ for

$(N, [zero, s u cc])$
$({0, 1}, [zero, f l i p])$

Definition. A morphism between two F-algebras $(X, α)$ and $(Y, β)$ is a morphism $f : X \to Y$ in $C$ such that the following diagram commutes:

Exercise. define a morphism of M-algebras

$(N, [zero, s u cc])$ to $({0, 1}, [zero, f l i p])$
- the mod2 function - to make the diagram commute

Algebras for a signature

An F $Σ$ -algebra is given by a map $α : ⋓_{i \in I} Σ_{n} \times A^{n} \to A$ . Then $(A, α)$ is just an algebra in standard notion

Coalgebras - the dual of algebras

Turning the arrows around, We will mess up with category

X → FX

Instead of constructors we start with destructors, how to destruct the state

Example. $N^{ω}$ is tht set of inifinite streams of natural numbers, $N^{ω} = {σ ∣ σ N \to N}$

Consider operations:

head : Nomega → N
tail : Nomega → Nomega
Then their paring: <head, tail> : Nomega → N x Nomega

so it fits a coalgebra structure for the functor: Str:Set → Set, defined by Str(X) = N \times X

Morphisms of clalgebras

Say we have another Str-coalgebra: where

h : Nomega \times Nomega -> N
t : Nomega \times Nomega -> Nomega \times Nomega

with h(sigma, tau) = sigma(O)              --- (identity)
and  t(sigma, tau) = (\tau, tail(sigma))

The coalgebra morphism? zip : Nomga \times Nomega -> N\omega that respects the structure

spoiler: zip is the final coalgebra, and we will use coinduction to prove that it is the unique one

think we are dualing in two aspects: the data/op filip and the finite/cofinte layout

Induction and Coinduction

Initial Algebras

F-algebras and their morphisms form a category Alg(F) Let F be a functor The initial F-algebra is an initial object in the category Alg(F)

Example. (N, [zero, succ]) is the initial algebra for the functor 1 + -

initial algebra ----> !exists morphism ---> arbitrary algebra

existece → definition by induction
uniqueness → proof by induction (List)A, [nil, cons] is the initial algebra for the functor TX = 1 + A times X

Dualize: Final coalgebra

F-coalgebras and their morphisms form a category Coalg(F) A final F-coalgebra is a final object in the category Coalg(F)

We have examples of coalgebras that don’t have final coalgebras

<Nomega, [head, tail]> is the final coalgebra for the functor Str(X) = N \times X

Exercise: even:

Algebras + coalgebras in preorders

a category C               |  a preorder (P, <=)
a functor F:C -> C         |  a monotone map f : P -> P
F-algebra: alpha : FX -> X |  pre-fixed point f(x) <= x
F-coalgbra: eps: X -> FX   | post-fixed point f(x) >= x
initial F-algebra          |  least pre-fixed point mu. f
final F-coalgebra          |  greatest post-fixed point nu. f

More examples

functor F : Set -> Set           | final coalgebra
FX = A \times X                  | <head,tail>: A^omega -> A \times A^omega
FX = 1 + A \times X              | A* + Aw -> 1 + A \times (A* + Aomega)
(with termination: finite list A* + infinite lists A\omega)
FX = P(X) (powerset)             | Non, recall Lambek Lemma
(Kripke frames, the same as giving relation between states)
FX = P(L \times X)               | Non, recall Lambek Lemma
(labelled transition systems)
(l, x') in F(x) means x' --->l x
FX = 2 \times X^A                | <eps, der> : 2^{A*} --> 2 \times 2^{A*}
(deterministic automata)
FX = 2 \times (P(X))^A           | No, if you stick to arbitrary powersets
(non-deterministic automata)
FX = (O \times X)^I              | casual functions I* --> O* 
(Mealy machine)

Coalgebras. can have finite structure, must infinite behavior e.g. X = {1, 2, 3}, A = {a, b}, \eps: X -> A * X State: x1|a --> x2|b --> x3|a --> x2|b ....

The final coalgebras will capture all the behavior of the systems modelled as F-coalgebras x_1 |-> a(ba)^omega

Compute initial algebras as colimits

Theorem (similar to Tarski) Let C be a category with an initial object O and colimits of w-chaines, Assume F preserves such colimits, then the colimit of the chain O ---!----> FO ----F!----> F^2O ----F^2!----> ... carries a structure of initial F-algebra (! for unique)

Example:
\Sigma = { o : 0, m : 2 } --- emp + binary operation
such that (F\sigma) X = { e } \times X^0  + { m } \times X ^2
						~~ { e }   + { m } \times X ^2

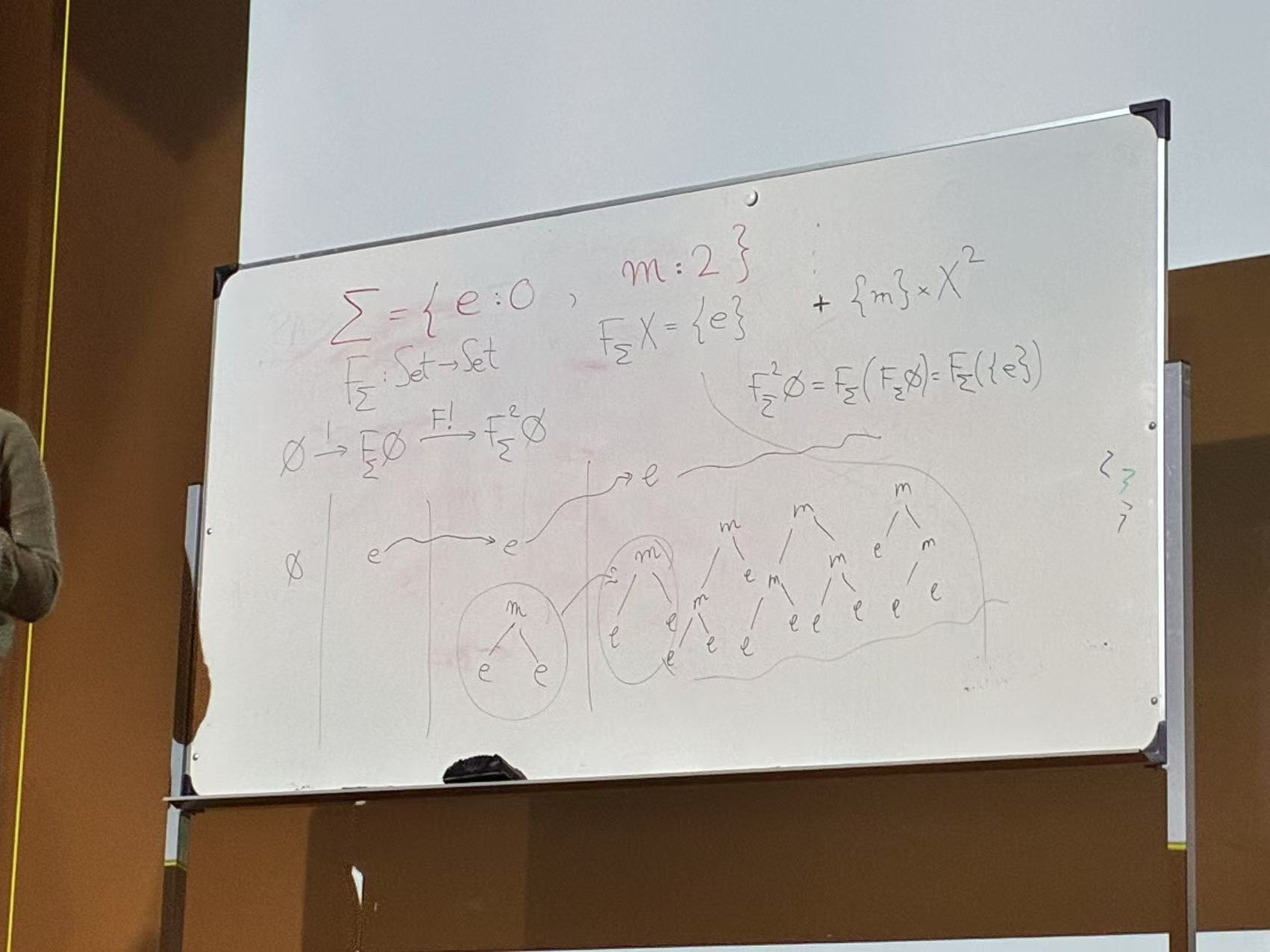
Computing final coalgebras as limits

Let C be a category with an final object 1 and limits of w^op chains. Assume F preserves such limits (in the proof, F L is also the limit, so we can invert the unique morphism, by def, L and FL are both the limit of the same chain), then the limit of the chain 1 <-!- F1 <-F!- F^2 1 <-- ... carries a structure of final F-coalgebra

Step 1 : L is the limit

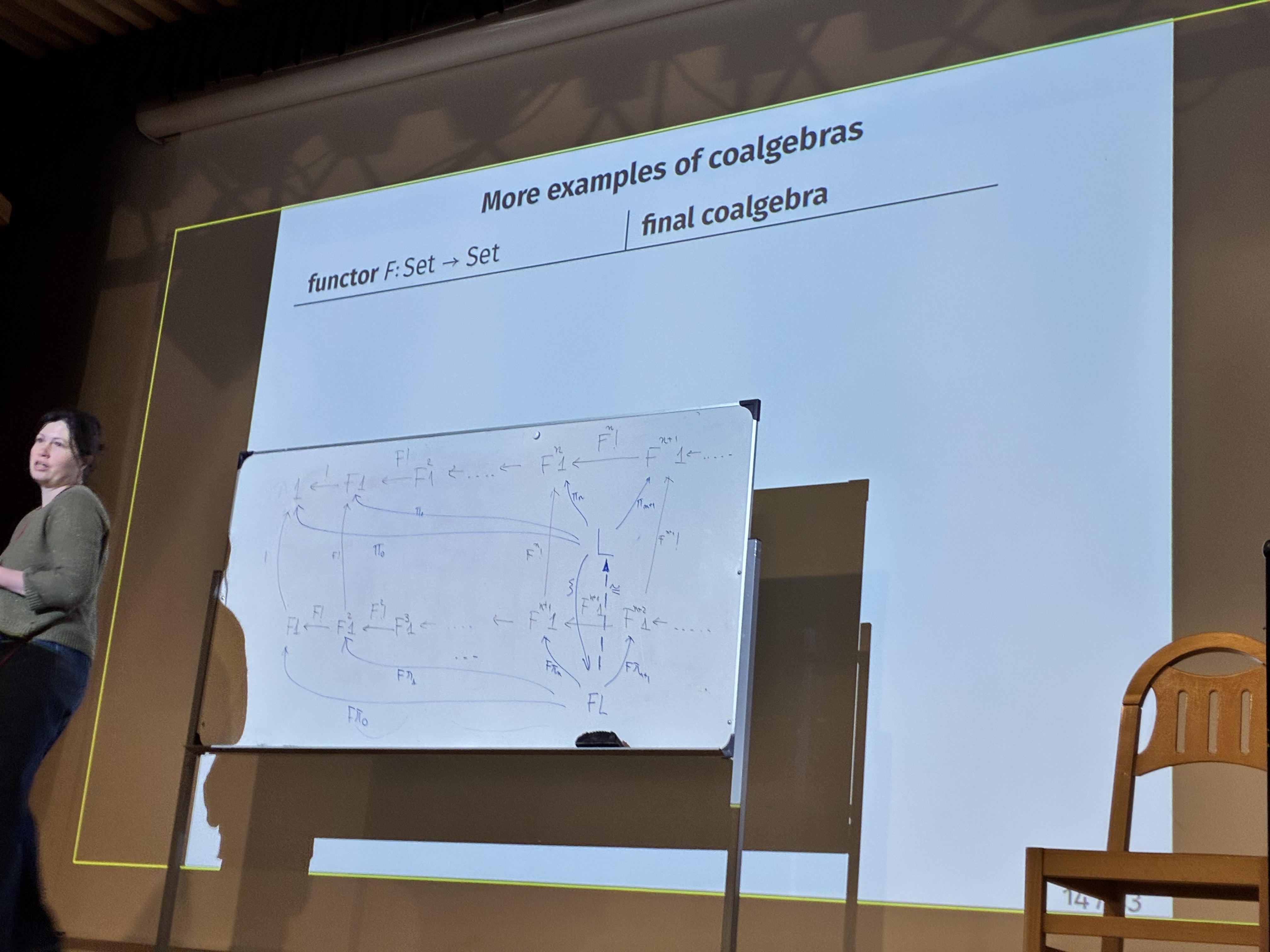Step 2 : for X ⇒ FX, show that there is a unique morphism from X to L, as L is the limit

Step 3: show the unique morphism from X to L commutes (exercise)

Congruence and bisimulations

F-congruence

induction proof principle

F-bisimulation

coinduction proof principle: every bisimulation on a fina F-coalgebra X → FX is contained in the diagonal on X

Examples

Labelled transition systems
Streams:
- R in X times Y is a bisuulation iff for all (x,y) in R we have hd_X(x) = hd_Y(y) and (tail_X(x), tail_Y(y)) in R

Several notions

Aczel-Mendler bisumulations
Hermida-Jacobs bisimulations See https://arxiv.org/pdf/1101.4223

Tony's Wiki

Explorer

May 19 Notes