A Categorical Approach to Automata Learning and Minimization

Author: Daniela Petrişan Institution: Université Paris Cité, IRIF, France Event: EPIT’25, Aussois Date: 20 May 2025 Source: Petrişan EPIT’25 Slides

---

References

• T. Colcombet and D. Petrişan, Automata minimization: a functorial approach. Log. Methods Comput. Sci., 16(1), 2020
• T. Colcombet, D. Petrisan, R. Stabile, Learning Automata and Transducers: A Categorical Approach. CSL 2021
• J. E. Pin (Ed.) Handbook of Automata Theory, EMS Press, 2021
• Further reading: Q. Aristote, S. van Gool, D. Petrişan, M. Shirmohammadi, Learning Weighted Automata over Number Rings, Concretely and Categorically. LICS 2025 (arXiv:2504.16596)

---

Tutorial Overview

This tutorial focuses on the interplay between category theory and automata theory. The categorical approach aims to:

• Provide a unifying framework for modelling various forms of automata.
• Obtain generic algorithms for learning.
• Highlight the link between automata learning and minimization.

---

Automata with Effects: A Categorical View

We can redefine various automata types by specifying a set of states Q and functions/arrows in a suitable category. The general structure involves an initial map, transition maps for each alphabet symbol, and a final map.

• Complete Deterministic Finite Automata (cDFA)

  • Given a set Q, an initial state $q_0:1\to Q$, transition functions ${\delta }_{\sigma }:Q\to Q$ for $\sigma \in A$, and a final state map ${\chi }_F:Q\to 2$ (where 2 is a two-element set for accept/reject).
  • Category: Set (sets and total functions).
  • Diagram: $1\stackrel{q_0}{\to }Q\stackrel{{\delta }_{\sigma }}{\to }Q\stackrel{{\chi }_F}{\to }2$.

• Deterministic Finite Automata (DFA) (possibly incomplete)

  • Given a set Q, an initial state $q_0:1\to Q$ (or $1\to 1+Q$), transition functions ${\delta }_{\sigma }:Q\to 1+Q$ (partial functions), and a final state map ${\chi }_F:Q\to 1+1$ (partial map to {accept}).
  • Category: Set• (sets and partial functions).
  • Diagram: $1\stackrel{q_0}{\to }Q\stackrel{{\delta }_{\sigma }}{\to }Q\stackrel{{\chi }_F}{\to }1$ (final map is to a singleton if only concerned with acceptance, often depicted as $Q\to 1+1$ or $Q\to \text{1}$ where $\text{1}$ is a terminal object with a partial map).

• Nondeterministic Finite Automata (NFA)

  • Given a set Q, initial states $I\subseteq Q$ (map $i:1\to \mathcal{P}(Q)$), transition relations ${\delta }_{\sigma }:Q\to \mathcal{P}(Q)$, and final states $F\subseteq Q$ (map $f:Q\to 2$ or $Q\to \mathcal{P}(1)$).
  • Category: Rel (sets and relations).
  • Diagram: $1\stackrel{i}{\to }Q\stackrel{{\delta }_{\sigma }}{\to }Q\stackrel{f}{\to }1$ (where arrows are relations; initial $1\to Q$ and final $Q\to 1$).

• Weighted Automata (WA) over a Semiring R

  • States Q form a basis for a free R-module $R^Q$.
  • Initial vector $i:R\to R^Q$, transition matrices (linear maps) ${\delta }_{\sigma }:R^Q\to R^Q$, and final vector $f:R^Q\to R$.
  • Category: FreeMod_R (R-modules and linear maps).
  • Diagram: $R\stackrel{i}{\to }{R}^Q\stackrel{{\delta }_{\sigma }}{\to }{R}^Q\stackrel{f}{\to }R$ (Often initial is $1\to R^Q$ or $R\to R^Q$ and final is $R^Q\to R$).

  linear map i: for entering initial state

  • transitions: give a matrix (linear transformation) = ${\Sigma }_i{\delta }_i{q}_i$
  • linear map fin for weight of leaving the final state

• Sequential Transducers (input alphabet A, output alphabet B)

  • States Q, initial state with initial output $i:1\to B^{\ast }\times Q+1$ (or $1\to 1+(B^{\ast }\times Q)$).
  • Transitions ${\delta }_{\sigma }:Q\to B^{\ast }\times Q+1$ for each $a\in A$.
  • Final outputs $f:Q\to B^{\ast }+1$.
  • An arrow $X\to Y$ is a function $X\to B^{\ast }\times Y+1$.

    1: for undefined states, B* for accepting words

  • Category: T (Kleisli category for $T(X)=B^{\ast }\times X+1$).

  related to the standard notion of Monad

  • Diagram: $1\stackrel{i}{\to }Q\stackrel{{\delta }_{\sigma }}{\to }Q\stackrel{f}{\to }1$ (arrows are $X\to 1+B^{\ast }\times Y$ or $X\to 1+B^{\ast }$).

We haven’t seen composition: why matters? for automata: accepting words

Automata	Category	Objects	Morphisms
complete DFAs	Sets	sets	functions
DFAs	Set_{\cdot}	sets	partial functions
NFA	Rel	sets	relations
WAs over R	FreeMod_R	R-modules	linear maps
subsequential transducers	…	…	… (we can construct, Kleisli category)

General Form: (C, I, O)-automata

• These are automata where initial (I), state (Q), and final (O) objects live in a category $\mathcal{C}$.
• Diagram: $I\stackrel{i}{\to }Q\stackrel{{\delta }_{\sigma }}{\to }Q\stackrel{f}{\to }O$.
  • I is considered as some initial object
  • O is considered as some final object

---

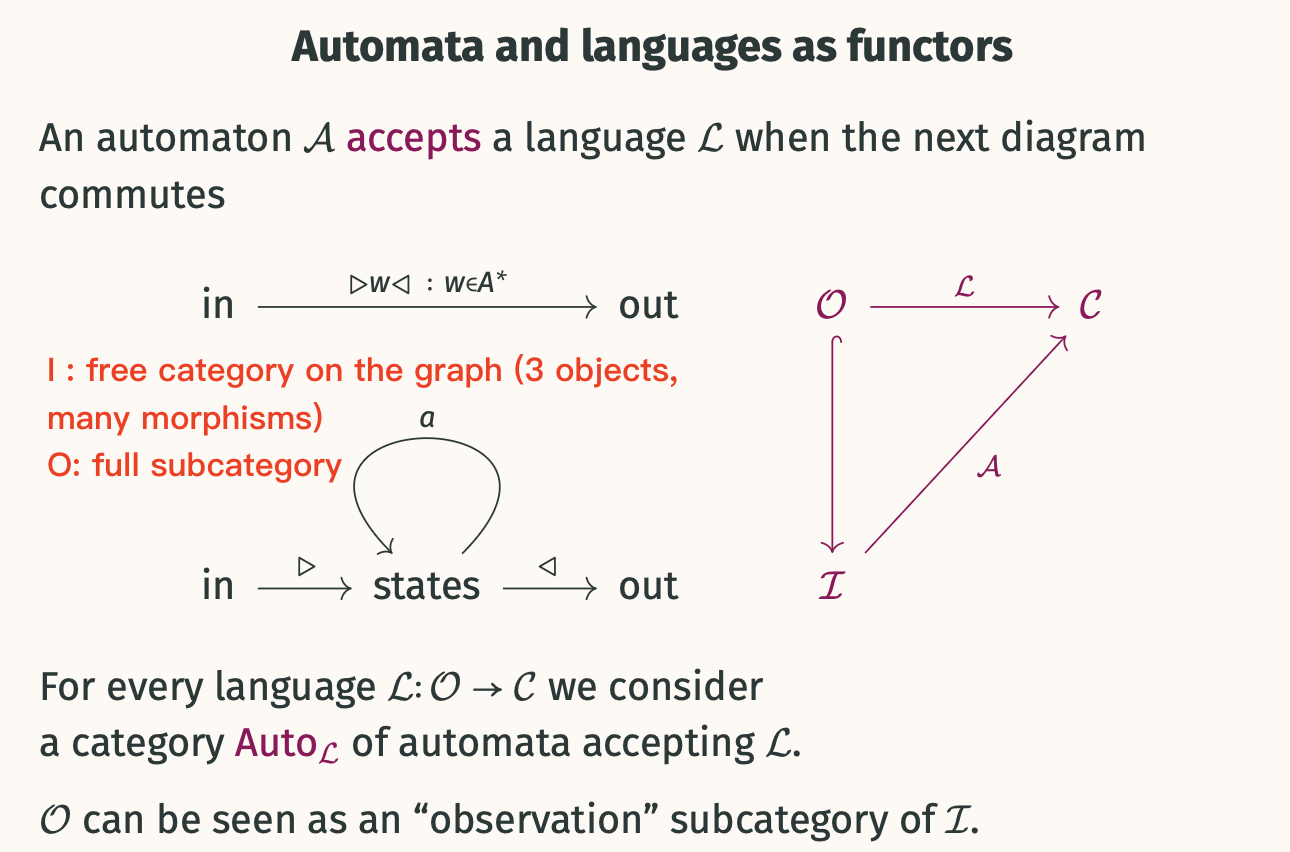
Word Automata as Functors

• Word automata on $A^{\ast }$ can be seen as functors $\mathcal{A}:\mathcal{I}\to \mathcal{C}$.
• The input category $\mathcal{I}$ is freely generated by objects states and arrows in: initial_object_placeholder \to states, out: states \to final_object_placeholder, and $\alpha :\text{states}\to \text{states}$ for each $\alpha \in A$.
• A functor $\mathcal{A}$ provides:
  • An object $Q=\mathcal{A}(\text{states})$ in $\mathcal{C}$.
  • An initial arrow $i:I\to Q$ (where I = \mathcal{A}(\text{initial_object_placeholder})).
  • A final arrow $f:Q\to F$ (where F = \mathcal{A}(\text{final_object_placeholder})).
  • Transition arrows ${\delta }_a:Q\to Q$ for each $a\in A$.
• The language accepted by $\mathcal{A}$ is a map $L_{\mathcal{A}}:A^{\ast }\to \mathcal{C}(I,F)$, where for $w=a_1...a_n$, $L_{\mathcal{A}}(w)=f\circ {\delta }_{a_n}\circ \cdots \circ {\delta }_{a_1}\circ i$.

this gives the standard notion for acceptance of words on all the above examples e.g.: for DFA, |I| = 1, |O| = 2, Set(1, 2) ~~ 2, so either accpept or reject, every word is mapped to some morphism from intial to final

• An automaton $\mathcal{A}$ accepts a language $\mathcal{L}$ (itself a functor $\mathcal{L}:\mathcal{O}\to \mathcal{C}$, where $\mathcal{O}$ is an observation subcategory of $\mathcal{I}$) if a specific diagram commutes.
• $Aut{o}_{\mathcal{L}}$ is the category of automata accepting $\mathcal{L}$.

Automata isomorphism ~~ natural transformation

---

Output Categories and Monads

The output categories seen so far (Set, Set•, Rel, Vec, T) are often Kleisli categories for monads T: Set $\to$ Set, specifying some effect:

• Set: Identity monad.
• Set• (partial functions): Maybe monad (option monad $X\mapsto 1+X$).
• Rel: Powerset monad ($\mathcal{P}X$) for non-determinism.
• T (sequential transducers): Monad of partial free actions of $B^{\ast }$ ($T(X)=B^{\ast }\times X+1$).

What in common? Answer. They are categories of free algebras (aka Kleisli categories) for monads specifying some effect: • the identity monad • the Maybe monad (aka option) • the powerset monad – non-determinism • the monad of partial free actions of _B_∗

PL perspective now!

---

Changing Output Categories via Adjunctions

Adjuction - For relating two categories in some way when they are not isomorphic

• Adjunction Recap: $F:\mathcal{C}\leftrightarrows \mathcal{D}:U$ with $F⊣U$ means natural isomorphisms $\mathcal{C}(X,UY)\cong \mathcal{D}(FX,Y)$.
  • $f:FX\to Y$ yields $f_b:X\to UY$.
  • $g:X\to UY$ yields $g^{\#}:FX\to Y$.
• Example 1 (Set vs Set•): $F:\text{Set}\leftrightarrows \text{Set•}:U$.
  • $FX=X$, $UX=1+X$.

  option monad:

• Example 2 (Set vs Rel): $F:\text{Set}\leftrightarrows \text{Rel}:U$.
  • $FX=X$, $UX=\mathcal{P}X$.

  powerset monad

• These are adjunctions between Set and $Kl(T)$, with $F$ identity on objects and $UX=TX$.

Lifting Adjunctions

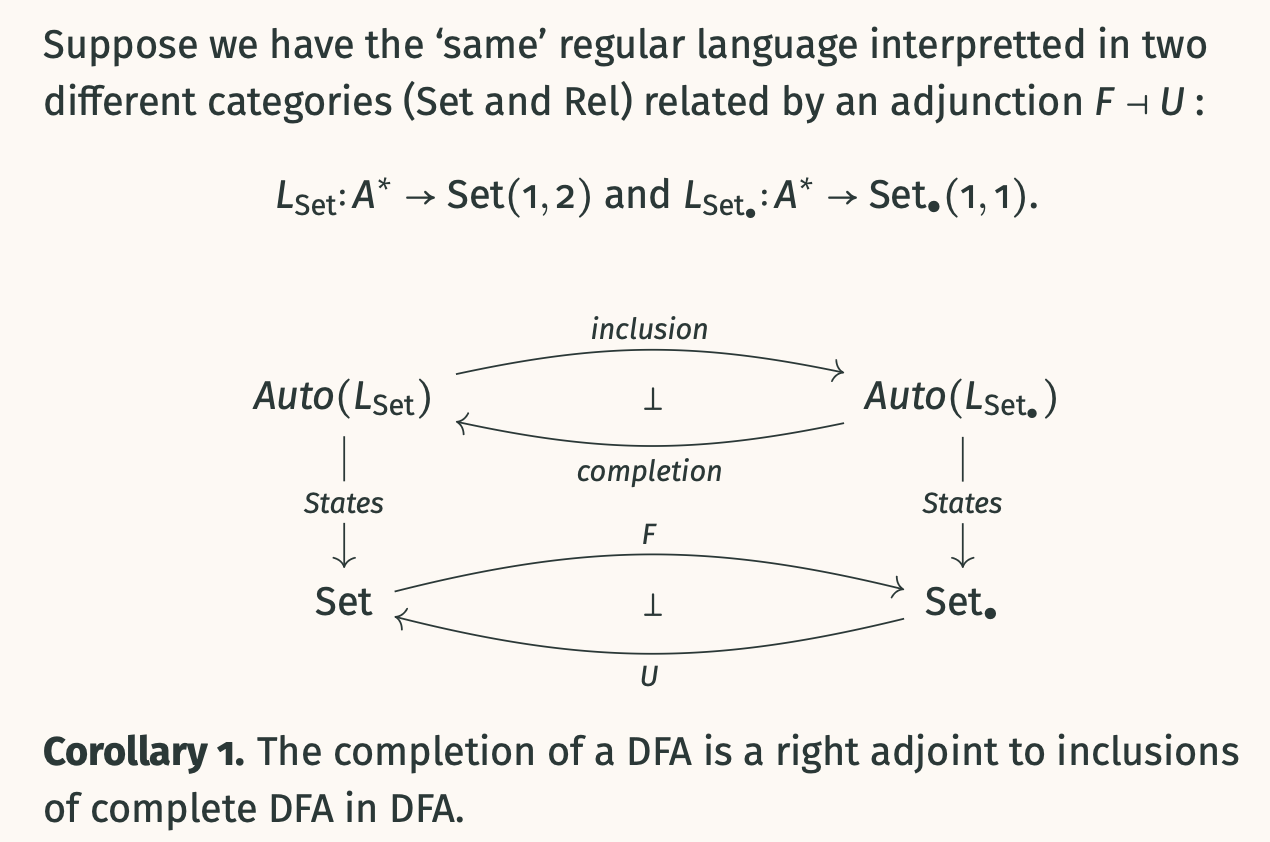
• If languages $L_C:A^{\ast }\to C(X,UY)$ and $L_D:A^{\ast }\to D(FX,Y)$ are “the same” under adjunction, there’s a relationship between $Auto(L_C)$ and $Auto(L_D)$.

Recall the map interpretation of language acceptance here

• Completing DFAs: The completion of a DFA is a right adjoint to the inclusion of complete DFAs into DFAs (adjunction between Set• and Set).

• Determinization of NFAs: Determinization (powerset construction) is a right adjoint to the inclusion of DFAs into NFAs (adjunction between Set and Rel).

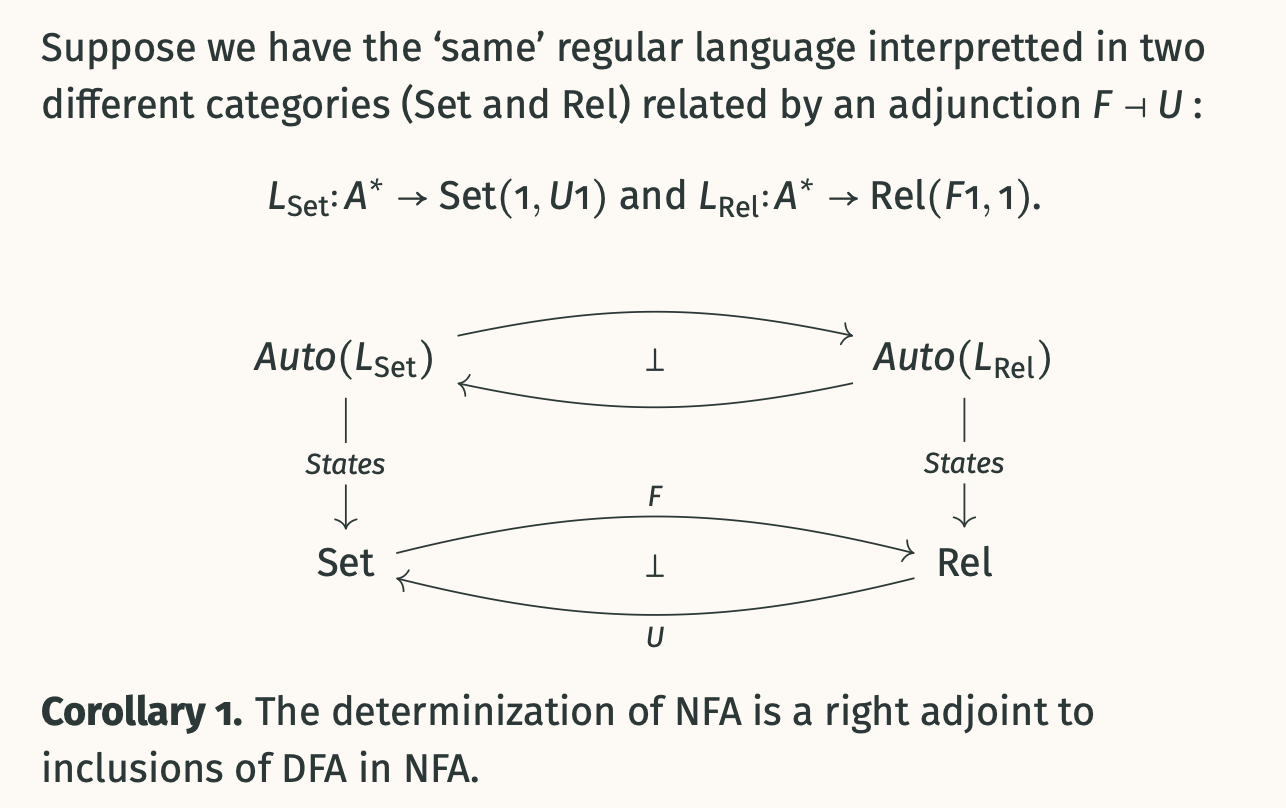
• Corollary 2. Initial automata are “free” in Kleisli-valued automata.

---

Automata Minimization: Categorical Perspective

Classical DFA Minimization

• Left Quotient: For $L\subseteq A^{\ast }$, $u^{-1}L=\{v\in A^{\ast }|uv\in L\}$.

aka language derivatives

• Myhill-Nerode Equivalence: $u{\equiv }_{L}v⟺u^{-1}L=v^{-1}L$.

Two words are equivalent if they have the same left quotient

• Myhill-Nerode Theorem: L is regular $⟺$ finitely many left quotients $⟺{\equiv }_L$ has finite index.
  • Proof idea:
    • $\Rightarrow$ If $\mathcal{A}=(Q,q_o,F,({\delta }_a))$ accepts L, then $(Q,{\delta }_u(q_o),F,({\delta }_a))$ accepts $u^{-1}L$.
    • $\Leftarrow$ Nerode Automaton: States are $\{u^{-1}L|u\in A^{\ast }\}$, initial state is $L$, final states are $\{u^{-1}L|u\in L\}$, ${\delta }_a(u^{-1}L)=(ua{)}^{-1}L$.
• Minimization Process for a DFA $\mathcal{A}$:
  1. Remove unreachable states $\to Reach(\mathcal{A})$.
  2. Merge states accepting the same language (indistinguishable) $\to Obs(Reach(\mathcal{A}))$.

Minimization of $\mathcal{C}$-Automata

What is the notion of minimal?

• A $\mathcal{C}$-automaton is minimal if it “divides” any other $\mathcal{C}$-automaton accepting the same language.

A DFA is minimal when it divides any other automaton accepting the same language. Here divides=«is a quotient of a sub-automaton of»

• “quotient” — “surjection for sets”
• “subobject” — “injection for sets”

• “Divides” means “is a quotient of a sub-automaton of”.
• This requires notions of “quotient” (surjection-like) and “subobject” (injection-like), i.e., a factorization system $(\mathcal{E},\mathcal{M})$ in $\mathcal{C}$.
  • $\mathcal{E}$ (epimorphisms/quotients), $\mathcal{M}$ (monomorphisms/subobjects).
  • Every morphism $f$ factors as $f=m\circ e$ with $e\in \mathcal{E},m\in \mathcal{M}$.
  • Factorization is unique up to isomorphism (functorial).

Three Ingredients for Categorical Minimization

For a language $\mathcal{L}:\mathcal{I}\to \mathcal{C}$, a minimal automaton $Min(\mathcal{L})$ exists if $Aut{o}_{\mathcal{L}}$ (the category of automata accepting $\mathcal{L}$) has:

1. An initial object ${\mathcal{A}}_{init}(\mathcal{L})$.
   • Exists if $\mathcal{C}$ has copowers (related to reachability).
   • For Set-DFAs: states $A^{\ast }$, $i:1\to A^{\ast }$ (maps to $ϵ$), ${\delta }_a(w)=wa$, $f:A^{\ast }\to 2$ (is $w\in L$?).
2. A final object ${\mathcal{A}}_{final}(\mathcal{L})$.
   • Exists if $\mathcal{C}$ has powers (related to observability).
   • For Set-DFAs: states $2^{A^{\ast }}$ (all possible languages), $i:1\to 2^{A^{\ast }}$ (maps to $L$), ${\delta }_a(K)=a^{-1}K$, $f:2^{A^{\ast }}\to 2$ (is $ϵ\in K$?).
3. A factorization system in $\mathcal{C}$. Then $Min(\mathcal{L})$ is obtained from the unique morphism $h:{\mathcal{A}}_{init}(\mathcal{L})\to {\mathcal{A}}_{final}(\mathcal{L})$ by factoring $h$ as ${\mathcal{A}}_{init}(\mathcal{L})\stackrel{e}{\to }Min(\mathcal{L})\stackrel{m}{\to }{\mathcal{A}}_{final}(\mathcal{L})$.

• For DFAs, $h:A^{\ast }\to 2^{A^{\ast }}$ is $w\mapsto w^{-1}L$. The factorization yields the Nerode automaton as $Min(\mathcal{L})$.
• This framework applies to R-weighted automata and sequential transducers (yielding Choffrut’s minimal transducer).
• $Min(\mathcal{L})$ divides any automaton $\mathcal{A}$ for $L$: ${\mathcal{A}}_{init}(L)\twoheadrightarrow reach(\mathcal{A})\twoheadrightarrow obs(reach(\mathcal{A}))\rightarrowtail {\mathcal{A}}_{final}(L)$, and $obs(reach(\mathcal{A}))$ maps to $Min(L)$.

---

Automata Learning: The $L^{\ast }$ Algorithm Categorically

• Goal: Learn a regular language L.
• Interaction: Learner asks Teacher:
  1. Membership queries: ”$w\in L$?“.
  2. Equivalence queries: “Does hypothesis automaton $H$ accept $L$?” If no, Teacher gives a counter-example.
• Algorithm maintains a pair of finite sets of words $(Q,T)$, starting with $(\{ϵ\},\{ϵ\})$.
  • $Q$: potential states (prefixes).
  • $T$: test words (suffixes) used for equivalence.
• T-equivalence (${\sim }_T$): $w{\sim }_{T}v⟺(\forall u\in T.wu\in L⟺vu\in L)$.
• Observation Table Conditions:
  • Closedness: $\forall q\in Q,\forall a\in A,\exists p\in Q\text{ such that }p{\sim }_{T}qa$. If not, add $qa$ to $Q$.
  • Consistency: $\forall q,q^{\prime }\in Q,\forall a\in A,(q{\sim }_T{q}^{\prime }⟹qa{\sim }_T{q}^{\prime }a)$. If not, find $u$ distinguishing $qau$ and $q^{\prime }au$, add $au$ to $T$.
• When $(Q,T)$ is closed and consistent, a hypothesis automaton $H(Q,T)$ can be built.

$L^{\ast }$ Revisited Categorically

• Learner has access to a fragment of the language $L_{Q,T}:Q{A}^{\ast }T\cup QT\to 2$ (boolean outcomes).
• This can be represented by a (Q,T)-biautomaton.
  • Diagram: $1\stackrel{▹q}{\to }{Q}_1\stackrel{a}{\to }{Q}_2\stackrel{ϵ}{\leftarrow }{Q}_1\stackrel{t◃}{\to }2$ (conceptual, $Q_1,Q_2$ are state objects derived from $Q,T$).
• Closure and consistency are encoded via the minimal (Q,T)-biautomaton.
  • The minimal (Q,T)-biautomaton is $1\stackrel{▹q_{min}}{\to }Q/{\sim }_T\cup AT\stackrel{a_{min}}{\to }(Q\cup QA)/{\sim }_T\stackrel{{ϵ}_{min}}{\leftarrow }Q/{\sim }_T\cup AT\stackrel{t{◃}_{min}}{\to }2$.
  • ${ϵ}_{min}$ is surjective $⟺(Q,T)$ is closed.
  • ${ϵ}_{min}$ is injective $⟺(Q,T)$ is consistent.
  • If ${ϵ}_{min}$ is an isomorphism, the two state objects are merged to form $H(Q,T)$.
• This yields a generic FunL* algorithm applicable to various automata types (DFAs, weighted automata over fields, sequential transducers).

FunL* Algorithm Sketch

1. Initialize $Q:=\{ϵ\}$, $T:=\{ϵ\}$.
2. Repeat:
   1. While ${ϵ}_{min}$ of the minimal (Q,T)-biautomaton is not an isomorphism (i.e., not closed or not consistent):
      • If not closed ( ${ϵ}_{min}\notin \mathcal{E}$ ), enlarge $Q$ (add $qa$ for some $q,a$).
      • If not consistent ( ${ϵ}_{min}\notin \mathcal{M}$ ), enlarge $T$ (add $au$ for some $a,u$ that breaks consistency).
   2. Build hypothesis $H(Q,T)$. Ask equivalence query.
   3. If Teacher answers NO with counterexample $w$: Add $w$ and its prefixes to $Q$.
3. Until Teacher answers YES. Return $H(Q,T)$.

---

Perspectives

• Explore conditions on a monad T such that $Kl(T)$ has properties for minimization/learning.

Problem with free algebras (not ideal): doesn’t have good factorizations / products

move to larger categories:

• Move to Eilenberg-Moore algebras (e.g., join-semilattices for Rel-valued automata) if $Kl(T)$ is not suitable.
• Extend to tree automata.
• Weighted automata over number rings.
• Learning nominal automata (building on work on automata in toposes).