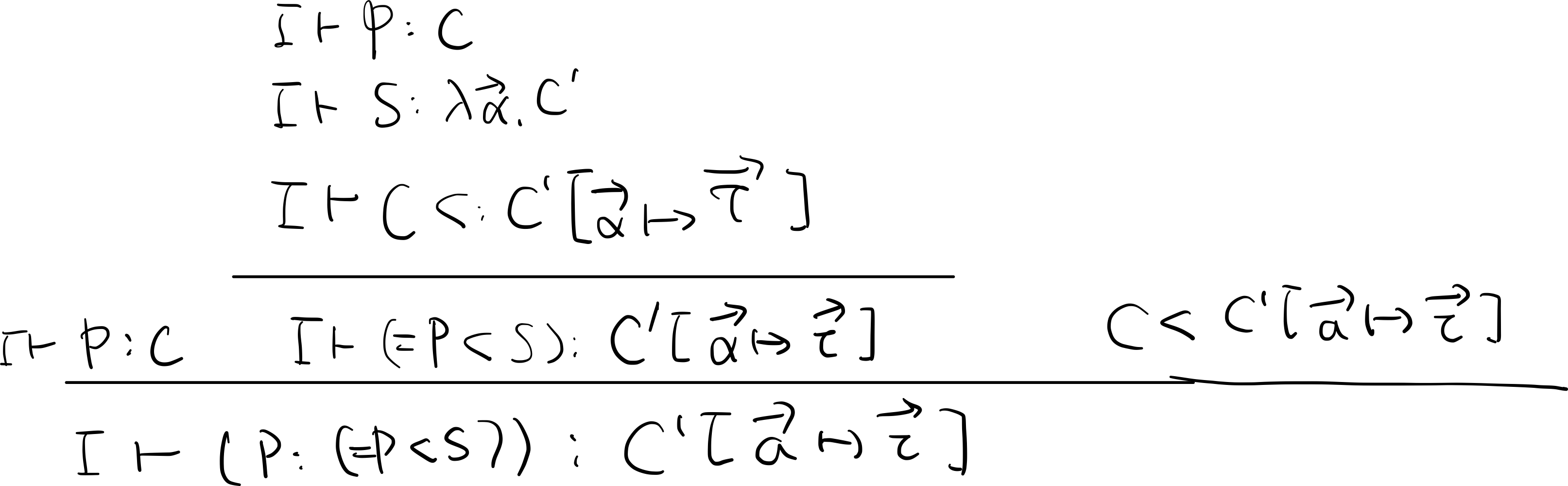Retrofitting and strengthening the ML module system

Jargon of Modules

1.1 Overview

4.1.2 Signature type-checking

Note: the type-checking is also an elaboration from source to Momega signatures

• declaration typing $\Gamma {⊢}_A\mathtt{D}:\lambda \bar{\alpha }.\mathcal{C}$
  • extrusion:
    • abstract type variables will be introduced in (type t = A.t) : \a. (type t = a)
    • for declarations, variables will be extruded and sequentially combied
    • for module type declarations, the binder is not lifted in its own scope
• signature typing $\Gamma ⊢\mathtt{S}:\lambda \bar{\alpha }.\mathcal{C}$
  • For sig ... end this is the last place where extrusion happens
  • M-Typ-Sig-LocalModType - look up local module type by path, see M-typ-decl-seq for how they are introduced
  • Transparent signatures: $\Gamma ⊢(=P<\mathtt{S}):\mathcal{C}[\bar{\alpha }\mapsto \bar{\tau }]$
    1. elaborate source signature $\mathtt{S}$ to $M^{\omega }$ signature $\lambda \bar{\alpha }.\mathcal{C}$
    2. infer the $P$ signature by module typing ${\mathcal{C}}^{\prime }$
    3. before subtyping check, find an instantiation, which is not easy in presence of higher-order types
    4. Check ${\mathcal{C}}^{\prime }<\mathcal{C}[\bar{\alpha }\mapsto \bar{\tau }]$
  • Generative functors $\to$ opaque existential signature
  • Applicative functors
    • Solution by F-ing modules
    • $⊢{\text{S}}_a:\lambda \bar{\alpha }.{\mathcal{C}}_a$
    • $\bar{\alpha },Y:{\mathcal{C}}_a⊢\mathtt{S}:\lambda \bar{\beta }.\mathcal{C}$
    • $⊢(Y:{\mathtt{S}}_a)\to \mathtt{S}:\lambda \overline{{\beta }^{\prime }}.\forall \bar{\alpha }.C\left[\bar{\beta }\mapsto \overline{{\beta }^{\prime }(\bar{\alpha })}\right]$
    • change $\bar{\beta }$ to higher order abstract types that can be applied to each universally quantified $\bar{\alpha }$
    • skolemization
  • For Momega, need to justify a similar skolemization but for the type of module expressions

4.1.3 Subtyping

= record subtyping + function subtyping + polymorphic subtyping (in universal + existential via instantiation)

• [[subtyping à la $F^{\eta }$]]

Implicit polymorphic subtyping:

Ψ ⊢τ Ψ ⊢[τ/a]A≤B
----------------

Ψ ⊢∀a.A≤B

We assume no subtyping in the core language

Question in the core language being used by the surface language, or no subtyping at all in the theory?

• submodules: simply propagtes down
• module type fields:
  • In F-ing modules, 2-way checking: allows for different ordering
  • Could have made: requiring same signature: up to Momega equivalence
  • adopted:
    • 2-way checking for the whole signature
    • require syntactic equality for dynamic parts (type definition / module type definition not checked)
• generative functors:
  • the right type can be more instantiated (that $\bar{\tau }$ can use the existential type on the left type vars $\bar{\alpha }$)
  • quite permissive to use
  • algorithmically challenging
    • potential lead to undecidability of subtyping
  • F-ing modules: several requirements for decidability

If we where to allow the user to input non-explicit signatures – either with an unrestricted module type of construct, or directly in Mω-signatures syntax – we would lose decidability. This hints at the fact that ML-modules are not just merely a mode of use of Fω (as written in F-ing (Rossberg et al. [2014])), but also a sweet spot, where changes seen as minor from Mω could easily break decidability.

4.1.4 Module Expression type-checking

• skolemization of applicative functors (module expressions) require transparent existential types
  • why not for types:

  • typing of signatures is just a mere manipulation of types where everything is possible, as long as the resulting signatures are wellformed. By contrast, for the typing of module expressions, the soundness relies on the ability to actually produce a term of the corresponding type

• propagation of modes
  • generative functors (abstraction, application) are opaque
  • applicative can be downgraded to generative
  • for structures, all bindings must have the same mode
• bindings typing the judgement of binding typing comes with a mode for tracking effects, but as in OCaml, it is user’s responsibility to mark generative functors
• paths: for looking up from the context, in checking the application of applicative functors
• ascription: introducing abstract types
  • difference, for: $(=P<S)$, the checking result is the instantiated one
  • for (P: S) te result is the (transparent) abstract type
  • The transparent ascription in OCaml (P <: S) is a syntax sugar of (P: (= P < S))
    • (= P < S) is the opaque ascription of P to the transparent signature #question What is exactly the behavior here

So, in OCaml actual usage, M-Typ-Mod-Ascr never creates new abstarct variables? The rule is generalized for proving? No? Typing for this syntax sugar:

• abstract-type binding also (the only other construct) introduces abstract-type binding
• Projection: thanks to $M^{\omega }$ signatures + lifted binders + paths inlined
  • we have a simple projection rule
  • there is another pass of garbage collection for avoiding useless abstract types

typechecking the projection of a submodule M.X is often a source of signature avoidance: the dependencies of the source signature of X might become dangling after the other components of the signature of M have been lost.

Section 4.2

• Source to source translation
  • add Id tags for module expressions/sig types,and prove that id field check can shortcut the equivalence check for the actual expression

Section 4.3

three anchoring conditions:

• ensure the $M^{\omega }$ signature is a valid elaboration result of a source
• functor application condition

Basically

• conditions for the first occurrence of type t = a
• conditions for module identities tag
• conditions for higher-order modules

and then a process of translating $M^{\omega }$ signatures to tagged source signatures and then an untagging process

Proved:

• Elaboration $\circ$ Anchoring = identity
• Anchoring $\circ$ Elaboration ~ identity`

Section 4.4

use explicitly typed $F^{\omega }$ + records + (transparent) existential types + predicative kind polymorphism (ensuring coherence)

• Same as F-ing modules, use identity functions to encode type fields (which carry additional typing constraints)

  • $⟨\tau ⟩=\Lambda \varphi .\lambda (x:\varphi \tau ).x$ the term
  • and its type $⟨\tau ⟩=\forall (\varphi :\kappa \to \star ).\varphi \tau \to \varphi \tau$

• Also the trick in F-ing modules, repack constructor for dealing with lifting open abstract type declarations to be visible in the rest of the program, since $F^{\omega }$ only supports non-dependent records

  • lift <a, x1 = e1 @ e2> = ... repack ...
  • and we have derived typing rule for lift function
  • (with a simple result existential type, where all abstract type variables are lifted to top-level)

• Lifting works for record types, but is not sufficient for applicative case (which uses skolemization)

  • lifting over universal types is not expressible
  • lifting over arrow types is unsound

• question does the F semantics with the modules semantics coincide?

• abstract signatures, fully supported?

  • Didier: this is the leaf
  • we can focus on abstract modules with only abstract types (level 0 - 1)
  • you will see the complexity of introducing abstract module types (level 2)
  • more advanced, issues with non-terminating subtyping checks (no use case?)